How do I trigger std::set's worst-case insert(), contains(), and remove() operations?

Question

I understand that the std::set is likely some sort of tree. I want to trigger std::set's worst-case insert(), contains(), and remove() operations - which I expect will take O(log(n)) time. I do not want to implement my own tree - I want to use std::set specifically.

In the image below, I perform these operations on std::set and the operations appear to be constant-time, on average. For bonus points, can anyone explain why this is constant instead of O(log(n))?

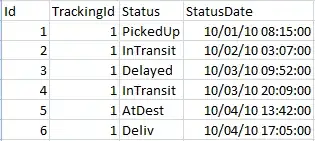
Below is my code measuring runtimes:

cout << "\n ................. Comparison: std::set vs. SortedQuickSet ..................\n ";
cout << "\n   Operation | # Elements | Total SQSetSet Runtime | Total std::set Runtime";
cout << "\n ------------|------------|------------------------|-----------------------\n";

for (int i = 0; i < COMPARISON_SET_DOUBLINGS; i++)
{
    set<unsigned> standardSet;
    SortedQuickSet sortedQuickSet;

    // Compare "Add" operations
    time = clock();                         // Start the timer
    for (unsigned j = 0; j < pow(2, i) * COMPARISON_SET_INITIAL_SIZE; j++) standardSet.insert((RANDOMIZED_SET_SIZE)-(rand() % (RANDOMIZED_SET_SIZE)));
    standardSetRuntime = clock() - time;    // Stop the timer
    time = clock();                         // Start the timer
    for (unsigned j = 0; j < pow(2, i) * COMPARISON_SET_INITIAL_SIZE; j++) sortedQuickSet.Add((RANDOMIZED_SET_SIZE)-(rand() % (RANDOMIZED_SET_SIZE)));
    SortedQuickSetRuntime = clock() - time; // Stop the timer
    cout << "         Add |";
    for (int j = 0; j < 18 - to_string(pow(2, i) * COMPARISON_SET_INITIAL_SIZE).length(); j++) cout << " ";
    cout << pow(2, i) * COMPARISON_SET_INITIAL_SIZE << " |";
    for (int j = 0; j < 23 - to_string(SortedQuickSetRuntime).length(); j++) cout << " ";
    cout << SortedQuickSetRuntime << " | " << standardSetRuntime << "  \n";

    // Compare "Contains" operations
    time = clock();                         // Start the timer
    for (unsigned j = 0; j < pow(2, i) * COMPARISON_SET_INITIAL_SIZE; j++) standardSet.find((RANDOMIZED_SET_SIZE)-(rand() % (RANDOMIZED_SET_SIZE)));
    standardSetRuntime = clock() - time;    // Stop the timer
    time = clock();                         // Start the timer
    for (unsigned j = 0; j < pow(2, i) * COMPARISON_SET_INITIAL_SIZE; j++) sortedQuickSet.Contains((RANDOMIZED_SET_SIZE)-(rand() % (RANDOMIZED_SET_SIZE)));
    SortedQuickSetRuntime = clock() - time; // Stop the timer
    cout << "    Contains |";
    for (int j = 0; j < 18 - to_string(pow(2, i) * COMPARISON_SET_INITIAL_SIZE).length(); j++) cout << " ";
    cout << pow(2, i) * COMPARISON_SET_INITIAL_SIZE << " |";
    for (int j = 0; j < 23 - to_string(SortedQuickSetRuntime).length(); j++) cout << " ";
    cout << SortedQuickSetRuntime << " | " << standardSetRuntime << "  \n";

    //// Compare "Get Sorted" operations
    //standardSetRuntime = 0;
    //time = clock();                           // Start the timer
    //for (auto element : standardSet) { }
    //standardSetRuntime = clock() - time;  // Stop the timer
    //SortedQuickSetRuntime = 0;
    //time = clock();                           // Start the timer
    //for (auto element : sortedQuickSet.Elements()) { }
    //SortedQuickSetRuntime = clock() - time;   // Stop the timer
    //cout << "  Get Sorted |";
    //for (int j = 0; j < 18 - to_string(pow(2, i) * COMPARISON_SET_INITIAL_SIZE).length(); j++) cout << " ";
    //cout << pow(2, i) * COMPARISON_SET_INITIAL_SIZE << " |";
    //for (int j = 0; j < 23 - to_string(SortedQuickSetRuntime).length(); j++) cout << " ";
    //cout << SortedQuickSetRuntime << " | " << standardSetRuntime << "  \n";

    // Compare "Remove" operations
    time = clock();                         // Start the timer
    for (unsigned j = 0; j < pow(2, i) * COMPARISON_SET_INITIAL_SIZE; j++) standardSet.erase((RANDOMIZED_SET_SIZE)-(rand() % (RANDOMIZED_SET_SIZE)));
    standardSetRuntime = clock() - time;    // Stop the timer
    time = clock();                         // Start the timer
    for (unsigned j = 0; j < pow(2, i) * COMPARISON_SET_INITIAL_SIZE; j++) sortedQuickSet.Remove((RANDOMIZED_SET_SIZE)-(rand() % (RANDOMIZED_SET_SIZE)));
    SortedQuickSetRuntime = clock() - time; // Stop the timer
    cout << "      Remove |";
    for (int j = 0; j < 18 - to_string(pow(2, i) * COMPARISON_SET_INITIAL_SIZE).length(); j++) cout << " ";
    cout << pow(2, i) * COMPARISON_SET_INITIAL_SIZE << " |";
    for (int j = 0; j < 23 - to_string(SortedQuickSetRuntime).length(); j++) cout << " ";
    cout << SortedQuickSetRuntime << " | " << standardSetRuntime;
    cout << "\n ------------|------------|------------------------|-----------------------\n";
}
cout << "\n Conclusion: on average, operations on a SortedQuickSet take ~30% as long as\n those on an std::set.";
cout << " Both set types perform these operations in constant\n time, and SortedQuickSet appears to have less overhead.\n";
cout << "\n ''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''\n\n ";

what do the numbers mean in your screenshot? did you warm up your cache? please be more specific on how you got to the idea that these operations perform in constant time. — BeyelerStudios, Aug 09 '15 at 17:02
I've updated my screenshot, thanks for pointing out its ambiguity. The (new) *total* operation cost numbers appear to double at the same rate that the number of elements does, suggesting that the operations are constant time. For example, if they were something like O(log(n)), I would expect to see them growing at a quicker rate than the number of elements. I didn't warm up my cache, nor do I know what that does. I'll look into it. — user3076399, Aug 09 '15 at 17:13
Cache warm-up means you run over your data multiple times to assert its been loaded into your CPU caches before measuring operation timings. What are the units for those measurements? Are they averages or single run? If you attached your measuring code to your post that would be helpful — BeyelerStudios, Aug 09 '15 at 17:22
The units of measurement are milliseconds (ms), and each time is the total amount of time it takes to perform the operation on a collection of elements. In my case, what would be the most effective way to warm-up my cache for each individual test (i.e. those of size 400, then size 800, etc.)? — user3076399, Aug 09 '15 at 17:27
In my opinion your date show O(n) - i.e. the runtime scales linearly with the problem size. If the operations were in constant time the run time should be independent of problem size - which is clearly not the case. — user422005, Aug 09 '15 at 17:33
@user422005 if the operations were constant time, then of course running `n` of those would grow linearly! — BeyelerStudios, Aug 09 '15 at 17:35
12000 isn't very many elements (it implies a tree depth of around 13), and a fairly easy to cache data set. Try 12 million or more. — Alan Stokes, Aug 09 '15 at 18:29
No new results after running on sets of 6 million, 12 million, and 24 million. http://i.imgur.com/5AztrZm.png — user3076399, Aug 09 '15 at 19:21

BeyelerStudios · Answer 1 · 2015-08-09T18:52:31.657

0

(note that you're evaluating the average runtimes with your tests, the worst case is impossible to find for an implementation dependant data structure like std::set)

I suspect that your pow and rand operations dominate your measurements:

time = clock();                         // Start the timer
for (unsigned j = 0; j < pow(2, i) * COMPARISON_SET_INITIAL_SIZE; j++) standardSet.insert((RANDOMIZED_SET_SIZE)-(rand() % (RANDOMIZED_SET_SIZE)));
standardSetRuntime = clock() - time;    // Stop the timer

should be

// determine test size
unsigned int N = (unsigned int)std::pow(2, i) * COMPARISON_SET_INITIAL_SIZE;
// build samples
std::vector<int> samples(N);
for (unsigned int j = 0; j < N; ++j)
    samples[j] = (RANDOMIZED_SET_SIZE)-(rand() % (RANDOMIZED_SET_SIZE));
for (unsigned int warmup = 0; warmup < 3; ++warmup) {
    // code warm-up (cache samples, cache instructions for insert)
    for (unsigned int j = 0; j < N; ++j)
        standardSet.insert(samples[j]);
    standardSet.clear();
}
// now measure
int* sample = &samples[0];
time = clock();                         // Start the timer
for (unsigned int j = 0; j < N; ++j)
    standardSet.insert(*sample++);
standardSetRuntime = clock() - time;    // Stop the timer

etc...

You'll probably note that the operations take nanoseconds now instead of milliseconds (rand was the most expensive part of your test -> there's exactly N rands -> runtime was growing linearly).

Also note that due to runtimes being affected by the data that you're actually inserting you should use the same samples for both data structures and to be more precise you should generate multiple sample-arrays, do your measurements for both on each array and then generate your statistics from those combined results. Otherwise you might randomly run into a preferred situation for one data structure but not the other.

You should get something like this:

edited Aug 09 '15 at 18:52

answered Aug 09 '15 at 17:35

BeyelerStudios

4,243
19
38

Here are the results of a run using the code above. It doesn't look like the changes impacted the runtimes (still appear to both be constant time). http://i.imgur.com/RVUuvyQ.png – user3076399 Aug 09 '15 at 17:53
@user3076399 hm strange, I get very log-like looking measurements (only tested `std::set.insert`): http://i.imgur.com/tpSl6zT.png – BeyelerStudios Aug 09 '15 at 18:50
@user3076399 I think you need a bigger `N` still, 400k just is very little data. – BeyelerStudios Aug 09 '15 at 19:18
No new results after running on sets of 6 million, 12 million, and 24 million. i.imgur.com/5AztrZm.png – user3076399 Aug 09 '15 at 19:23
Same code, just changed a global variable: const unsigned COMPARISON_SET_INITIAL_SIZE = 6000000; const unsigned COMPARISON_SET_DOUBLINGS = 3; – user3076399 Aug 09 '15 at 19:39
I mean show me how you implemented my changes: are you only measuring `standardSet.insert(*sample++);` in a loop? – BeyelerStudios Aug 09 '15 at 19:49
I copy-pasted your code into mine, like this: time = clock(); for (unsigned int j = 0; j < N; ++j) {standardSet.insert(samples[j]);} standardSetRuntime = clock() - time; – user3076399 Aug 09 '15 at 19:59
@user3076399 next thing you can do is replace the set.insert code with something you know is logarithmic, like bisection ([binary_search](http://en.cppreference.com/w/cpp/algorithm/binary_search) an array from 1..N for random positions p in [1..N]). If that gives expected logarithmic timings, you should inspect the implementation of your std::set – BeyelerStudios Aug 09 '15 at 20:14
btw. how large is `RANDOMIZED_SET_SIZE`? – BeyelerStudios Aug 09 '15 at 20:15

How do I trigger std::set's worst-case insert(), contains(), and remove() operations?

1 Answers1