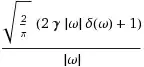-1

I have been having a big problem understanding the concept of numerical ifft.

Consider a function in spatial domain like f(x)=-2/pi*Ln(abs(x)) in which x is between -Lx and Lx. The fourier transform of this function is F(w)=2/abs(w).

I want to figure out whether these two are numerically the same using ifft command in Matlab. If you run the simple code below, you will see the difference that bothers me:

  clc

  clear all

  Lx=0.0005;

  N=pow2(10);

  dx=2*Lx/(N-1);

  w=pi/(N*dx)*linspace(-N/2,N/2,N);

  Hw=2./abs(w);

  hx=1/dx*abs(fftshift(ifft(Hw)));

  x=linspace(-Lx,Lx,N);

  hxexact=-2/pi.*log(abs(x));

  plot(x,hx,x,hxexact,'r')

  legend('ifft','exact')

here is the output:

I would appreciate that if anyone could help me with this.

Mohammad Bazrafshan
  • 51
  • 4
  • 1
    Please add the output and explain what you expect and what you get. I won't run random matlab scripts just to understand SO questions. – usr1234567 Jul 16 '15 at 09:14
  • I meant to add the output (the graph) but apparently I am not allowed because I need to have at least 10 reputations (as the admin pops up an error). – Mohammad Bazrafshan Jul 16 '15 at 10:04
  • Then describe the graph or post some values. We still don't know what you expect and what you get. – usr1234567 Jul 16 '15 at 10:07
  • The fourier transform of f(x) is F(w). I want to figure out whether the ifft of F(w) is the same as f(x). In the code above Hw is the fourier transform of the function. Applying the ifft on Hw leads to hx which must be the same as hxexact (the analytical f(x), the exact function in spatial domain). But they are not the same, unfortunately. I cannot understand where the problem is. The vectorized output is too long for N=2^10 but for N=2^4, the results are as: – Mohammad Bazrafshan Jul 16 '15 at 10:35
  • hx hexact 0 4.8389 0.2368 4.9300 0.4792 5.0363 0.7514 5.1641 1.0457 5.3241 1.4357 5.5383 1.9015 5.8635 2.8538 6.5629 4.8267 6.5629 2.8538 5.8635 1.9015 5.5383 1.4357 5.3241 1.0457 5.1641 0.7514 5.0363 0.4792 4.9300 0.2368 4.8389 – Mohammad Bazrafshan Jul 16 '15 at 10:43

1 Answers1

0

You seem to have some confusion about the FFT for your function, the result you might have been looking for is:

sqrt(2./pi) / w

This is the fft of your function IFF w is positive!

This is the FFT in the general case:

This is the FFT in the general case

If you use MATLAB's fft function instead of using your own 2./abs(w) you will see that the ifft and the original function align.

Tim B
  • 3,033
  • 1
  • 23
  • 28
  • Thanks a lot Tim. In the practical case that I am working on, I don't what f(x) is and I should generate it by ifft on F(w) which is available to me as an analytical function. Just to make sure that I am using ifft in the correct way, I need to validate my procedure with this simple problem in which I know its original function in the spatial domain. This function and its transform have been chosen from a paper in this regard. It is like a reconstructing a time series signal through ifft and by having in hand only the magnitude of the spectrum and not the phase data. – Mohammad Bazrafshan Jul 16 '15 at 12:38