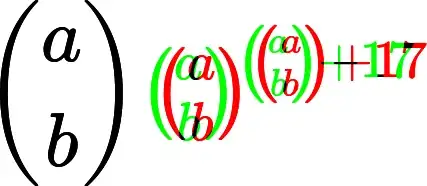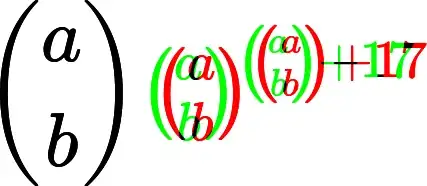How to perform discrete optimization of functions over matrices?

Question

I would like to optimize over all 30 by 30 matrices with entries that are 0 or 1. My objective function is the determinant. One way to do this would be some sort of stochastic gradient descent or simulated annealing.

I looked at scipy.optimize but it doesn't seem to support this sort of optimization as far as I can tell. scipy.optimize.basinhopping looked very tempting but it seems to require continuous variables.

Are there any tools in Python for this sort of general discrete optimization?

Answer 1

I think a genetic algorithm might work quite well in this case. Here's a quick example thrown together using deap, based loosely on their example here:

import numpy as np
import deap
from deap import algorithms, base, tools
import imp


class GeneticDetMinimizer(object):

    def __init__(self, N=30, popsize=500):

        # we want the creator module to be local to this instance, since
        # creator.create() directly adds new classes to the module's globals()
        # (yuck!)
        cr = imp.load_module('cr', *imp.find_module('creator', deap.__path__))
        self._cr = cr

        self._cr.create("FitnessMin", base.Fitness, weights=(-1.0,))
        self._cr.create("Individual", np.ndarray, fitness=self._cr.FitnessMin)

        self._tb = base.Toolbox()

        # an 'individual' consists of an (N^2,) flat numpy array of 0s and 1s
        self.N = N
        self.indiv_size = N * N

        self._tb.register("attr_bool", np.random.random_integers, 0, 1)
        self._tb.register("individual", tools.initRepeat, self._cr.Individual,
                          self._tb.attr_bool, n=self.indiv_size)

        # the 'population' consists of a list of such individuals
        self._tb.register("population", tools.initRepeat, list,
                          self._tb.individual)
        self._tb.register("evaluate", self.fitness)
        self._tb.register("mate", self.crossover)
        self._tb.register("mutate", tools.mutFlipBit, indpb=0.025)
        self._tb.register("select", tools.selTournament, tournsize=3)

        # create an initial population, and initialize a hall-of-fame to store
        # the best individual
        self.pop = self._tb.population(n=popsize)
        self.hof = tools.HallOfFame(1, similar=np.array_equal)

        # print summary statistics for the population on each iteration
        self.stats = tools.Statistics(lambda ind: ind.fitness.values)
        self.stats.register("avg", np.mean)
        self.stats.register("std", np.std)
        self.stats.register("min", np.min)
        self.stats.register("max", np.max)

    def fitness(self, individual):
        """
        assigns a fitness value to each individual, based on the determinant
        """
        return np.linalg.det(individual.reshape(self.N, self.N)),

    def crossover(self, ind1, ind2):
        """
        randomly swaps a subset of array values between two individuals
        """
        size = self.indiv_size
        cx1 = np.random.random_integers(0, size - 2)
        cx2 = np.random.random_integers(cx1, size - 1)
        ind1[cx1:cx2], ind2[cx1:cx2] = (
            ind2[cx1:cx2].copy(), ind1[cx1:cx2].copy())
        return ind1, ind2

    def run(self, ngen=int(1E6), mutation_rate=0.3, crossover_rate=0.7):

        np.random.seed(seed)
        pop, log = algorithms.eaSimple(self.pop, self._tb,
                                       cxpb=crossover_rate,
                                       mutpb=mutation_rate,
                                       ngen=ngen,
                                       stats=self.stats,
                                       halloffame=self.hof)
        self.log = log
        return self.hof[0].reshape(self.N, self.N), log

if __name__ == "__main__":
    np.random.seed(0)
    gd = GeneticDetMinimizer()
    best, log = gd.run()

It takes about 40 seconds to run 1000 generations on my laptop, which gets me from a minimum determinant value of about -5.7845x10⁸ to -6.41504x10¹¹. I haven't really played around much with the meta-parameters (population size, mutation rate, crossover rate etc.), so I'm sure it's possible to do a lot better.

---

Here's a greatly improved version that implements a much smarter crossover function that swaps blocks of rows or columns across individuals, and uses a cachetools.LRUCache to guarantee that each mutation step produces a novel configuration, and to skip evaluation of the determinant for configurations that have already been tried:

import numpy as np
import deap
from deap import algorithms, base, tools
import imp
from cachetools import LRUCache

# used to control the size of the cache so that it doesn't exceed system memory
MAX_MEM_BYTES = 11E9


class GeneticDetMinimizer(object):

    def __init__(self, N=30, popsize=500, cachesize=None, seed=0):

        # an 'individual' consists of an (N^2,) flat numpy array of 0s and 1s
        self.N = N
        self.indiv_size = N * N

        if cachesize is None:
            cachesize = int(np.ceil(8 * MAX_MEM_BYTES / self.indiv_size))

        self._gen = np.random.RandomState(seed)

        # we want the creator module to be local to this instance, since
        # creator.create() directly adds new classes to the module's globals()
        # (yuck!)
        cr = imp.load_module('cr', *imp.find_module('creator', deap.__path__))
        self._cr = cr

        self._cr.create("FitnessMin", base.Fitness, weights=(-1.0,))
        self._cr.create("Individual", np.ndarray, fitness=self._cr.FitnessMin)

        self._tb = base.Toolbox()
        self._tb.register("attr_bool", self.random_bool)
        self._tb.register("individual", tools.initRepeat, self._cr.Individual,
                          self._tb.attr_bool, n=self.indiv_size)

        # the 'population' consists of a list of such individuals
        self._tb.register("population", tools.initRepeat, list,
                          self._tb.individual)
        self._tb.register("evaluate", self.fitness)
        self._tb.register("mate", self.crossover)
        self._tb.register("mutate", self.mutate, rate=0.002)
        self._tb.register("select", tools.selTournament, tournsize=3)

        # create an initial population, and initialize a hall-of-fame to store
        # the best individual
        self.pop = self._tb.population(n=popsize)
        self.hof = tools.HallOfFame(1, similar=np.array_equal)

        # print summary statistics for the population on each iteration
        self.stats = tools.Statistics(lambda ind: ind.fitness.values)
        self.stats.register("avg", np.mean)
        self.stats.register("std", np.std)
        self.stats.register("min", np.min)
        self.stats.register("max", np.max)

        # keep track of configurations that have already been visited
        self.tabu = LRUCache(cachesize)

    def random_bool(self, *args):
        return self._gen.rand(*args) < 0.5

    def mutate(self, ind, rate=1E-3):
        """
        mutate an individual by bit-flipping one or more randomly chosen
        elements
        """
        # ensure that each mutation always introduces a novel configuration
        while np.packbits(ind.astype(np.uint8)).tostring() in self.tabu:
            n_flip = self._gen.binomial(self.indiv_size, rate)
            if not n_flip:
                continue
            idx = self._gen.random_integers(0, self.indiv_size - 1, n_flip)
            ind[idx] = ~ind[idx]
        return ind,

    def fitness(self, individual):
        """
        assigns a fitness value to each individual, based on the determinant
        """
        h = np.packbits(individual.astype(np.uint8)).tostring()
        # look up the fitness for this configuration if it has already been
        # encountered
        if h not in self.tabu:
            fitness = np.linalg.det(individual.reshape(self.N, self.N))
            self.tabu.update({h: fitness})
        else:
            fitness = self.tabu[h]
        return fitness,

    def crossover(self, ind1, ind2):
        """
        randomly swaps a block of rows or columns between two individuals
        """

        cx1 = self._gen.random_integers(0, self.N - 2)
        cx2 = self._gen.random_integers(cx1, self.N - 1)
        ind1.shape = ind2.shape = self.N, self.N

        if self._gen.rand() < 0.5:
            # row swap
            ind1[cx1:cx2, :], ind2[cx1:cx2, :] = (
                ind2[cx1:cx2, :].copy(), ind1[cx1:cx2, :].copy())
        else:
            # column swap
            ind1[:, cx1:cx2], ind2[:, cx1:cx2] = (
                ind2[:, cx1:cx2].copy(), ind1[:, cx1:cx2].copy())

        ind1.shape = ind2.shape = self.indiv_size,

        return ind1, ind2

    def run(self, ngen=int(1E6), mutation_rate=0.3, crossover_rate=0.7):

        pop, log = algorithms.eaSimple(self.pop, self._tb,
                                       cxpb=crossover_rate,
                                       mutpb=mutation_rate,
                                       ngen=ngen,
                                       stats=self.stats,
                                       halloffame=self.hof)
        self.log = log

        return self.hof[0].reshape(self.N, self.N), log

if __name__ == "__main__":
    np.random.seed(0)
    gd = GeneticDetMinimizer(0)
    best, log = gd.run()

My best score thus far is about -3.23718x10¹³ -3.92366x10¹³ after 10000 1000 generations, which takes about 45 seconds on my machine.

Based on the solution cthonicdaemon linked to in the comments, the maximum determinant for a 31x31 Hadamard matrix must be at least 75960984159088×2³⁰ ~= 8.1562x10²² (it's not yet proven whether that solution is optimal). The maximum determinant for an (n-1 x n-1) binary matrix is 2^1-n times the value for an (n x n) Hadamard matrix, i.e. 8.1562x10²² x 2^-30 ~= 7.5961x10¹³, so the genetic algorithm gets within an order of magnitude of the current best known solution.

However, the fitness function seems to plateau around here, and I'm having a hard time breaking -4x10¹³. Since it's a heuristic search there is no guarantee that it will eventually find the global optimum.

Answer 2

I don't know of any straight-forward method for discrete optimization in scipy. One alternative is using the simanneal package from pip or github, which allows you to introduce your own move function, such that you can restrict it to moves within your domain:

import random
import numpy as np
import simanneal

class BinaryAnnealer(simanneal.Annealer):

    def move(self):
        # choose a random entry in the matrix
        i = random.randrange(self.state.size)
        # flip the entry 0 <=> 1
        self.state.flat[i] = 1 - self.state.flat[i]

    def energy(self):
        # evaluate the function to minimize
        return -np.linalg.det(self.state)

matrix = np.zeros((5, 5))
opt = BinaryAnnealer(matrix)
print(opt.anneal())

Answer 3

I have looked into this a bit.

A couple of things first off: 1) 56 million is the max value when the size of the matrix is 21x21, not 30x30:https://en.wikipedia.org/wiki/Hadamard%27s_maximal_determinant_problem#Connection_of_the_maximal_determinant_problems_for_.7B1.2C.C2.A0.E2.88.921.7D_and_.7B0.2C.C2.A01.7D_matrices.

But that is also an upper bound on -1, 1 matrices, not 1,0.

EDIT: Reading more carefully from that link:

The maximal determinants of {1, −1} matrices up to size n = 21 are given in the following table. Size 22 is the smallest open case. In the table, D(n) represents the maximal determinant divided by 2n−1. Equivalently, D(n) represents the maximal determinant of a {0, 1} matrix of size n−1.

So that table can be used for upper bounds, but remember they're divided by 2n−1. Also note that 22 is the smallest open case, so trying to find the maximum of a 30x30 matrix has not been done, and is not even close to being done just yet.

2) The reason David Zwicker's code gives an answer of 30 million is probably due to the fact that he's minimising. Not maximising.

return -np.linalg.det(self.state)

See how he's got the minus sign there?

3) Also, the solution space for this problem is very big. I calculate the number of different matrices to be 2^(30*30) i.e. in the order of 10^270. So looking at each matrix is simply impossible, and even look at most of them is too.

I have a bit of code here (adapted from David Zwicker's code) that runs, but I have no idea how close it is to the actual maximum. It takes around 45 mins to do 10 million iterations on my PC, or only about 2 mins for 1 mill iterations. I get a max value of around 3.4 billion. But again, I have no idea how close this is to the theoretical maximum.

import numpy as np
import random
import time

MATRIX_SIZE = 30


def Main():

    startTime = time.time()
    mat = np.zeros((MATRIX_SIZE, MATRIX_SIZE), dtype = int)
    for i in range(MATRIX_SIZE):
        for j in range(MATRIX_SIZE):
            mat[i,j] = random.randrange(2)

    print("Starting matrix:\n", mat)       

    maxDeterminant = 0

    for i in range(1000000):
        # choose a random entry in the matrix
        x = random.randrange(MATRIX_SIZE)
        y = random.randrange(MATRIX_SIZE)

    mat[x,y] = 1 - mat[x,y]

        #print(mat)

        detValue = np.linalg.det(mat)
        if detValue > maxDeterminant:
            maxDeterminant = detValue


    timeTakenStr = "\nTotal time to complete: " + str(round(time.time() - startTime, 4)) + " seconds"
    print(timeTakenStr )
    print(maxDeterminant)


Main()

Does this help?