How can I highlight variance over a ggplot?

Question

I can't find out how should I put up this ques so I used this method.

I have a latitude-longitude dataset. The image posted below is what I want to produce.. This is my dataset:

Latitude    Longitude
21.06941667 71.07952778
21.06941667 71.07952778
21.06666667 71.08158333
21.07186111 71.08688889
21.08625    71.07083333
21.08719444 71.07286111
21.08580556 71.07686111
21.07894444 71.08225
....

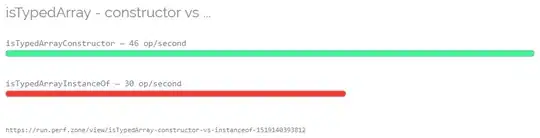
enter image description here

I have used geom_path() to find the path. Now, As shown in fig. I have highlighted the variance with white color around the path which I want to do. This is how I calculated variance:

var.latitude <- var(Data$Latitude)
var.longitude <- var(Data$Longitude)

I have marked the variance over the points using geom_errorbar():

geom_errorbar(aes(x=Latitude,y=Longitude, ymin=Longitude-var.longitude, ymax=Longitude+var.longitude),width=0.001)+
geom_errorbarh(aes(xmin=Latitude-var.latitude,xmax=Latitude+var.latitude),height=0.001)

Can anyone tell me how should I highlight the white area?

you *could* add a thick white path `geom_path(data=Data, aes(x=Latitude, y=Longitude), size=8, colour="white")` — tospig, Jul 05 '15 at 08:59
@tospig I can't just thick the path using size. I need variance for that — ayush, Jul 05 '15 at 21:23
@tospig Yes.. May be! but I have 2 different variance. i.e., latitude and longitue. I can't use both lat/long simultaneously in this. — ayush, Jul 05 '15 at 22:36
@ayush Using trigonometric reasonsing you should be able to calculate an approrpiate local width resembling you illustration? — CMichael, Jul 06 '15 at 06:52
@CMichael can you help me with an example. I really didn't get what you mean to explain. — ayush, Jul 06 '15 at 07:03
I see what you mean now. You could write code to go from point-to-point, look at the 4 vertices per point, and find the fattest min-max line each time. Not too difficult, but I don't have the time to invest in that now. Maybe later in the week if no one else does it. — Mike Wise, Jul 06 '15 at 12:40
Please provide reproducible R script for analysis purpose so that we can get to it quickly, thanks. — Henry.L, Jul 07 '15 at 08:55
@Henry.L you can take any data for lat/long values for similar dataset. — ayush, Jul 07 '15 at 09:03
This is actually quite complicated. You need to trace the outline of the white area, but there's no simple rule of how the coordinates of vertex are calculated based on lat., long., and the variances. Instead, one has to keep track of the direction in which one is tracing, etc. Doable, but a significant investment of time and effort. — Claus Wilke, Jul 08 '15 at 01:02
@ClausWilke Think it like this. Take the original path() as the refrence line and plot the variance around this refrence line. Yes, the coordinates for lat/long are rondom. Can you solve the problem please? I am stucked in this problem for a verylong time. — ayush, Jul 08 '15 at 03:52

mts · Accepted Answer · 2016-01-17T08:31:31.410

I'm approaching this with the polygon feature of ggplot, see the documentation

library(ggplot2)    
data = rbind.data.frame(c(21.06941667, 71.07952778),
                        c(21.06666667, 71.08158333 ),
                        c(21.07186111, 71.08688889 ),
                        c(21.08625   , 71.07083333 ),
                        c(21.08719444, 71.07286111 ),
                        c(21.08580556, 71.07686111 ),
                        c(21.07894444, 71.08225 ))
names(data) = c("Latitude",     "Longitude")

Your variance is quite small, I multiplied by 10 for it to be visible in the graph. Note that in the graph in your question you draw the area from the fins of the errorbars, which is almost certainly not what you want.

var.latitude <- var(data$Latitude)*10
var.longitude <- var(data$Longitude)*10

Calculating this area as one is a menial task as also noted in the comments above. I found the easiest way to do this is overlapping two polygons for each path plus a polygon for each point. There sure may be more elegant ways, but hey, it works.

pos.poly = data.frame(id = paste0("c", as.character(1)), 
                      x = c(data$Latitude[1]-var.latitude, data$Latitude[1], data$Latitude[1]+var.latitude, data$Latitude[1]), 
                      y = c(data$Longitude[1], data$Longitude[1]+var.longitude, data$Longitude[1], data$Longitude[1]-var.longitude))
for(i in 2:dim(data)[1]){
  loc.pos1 = data.frame(id = paste0("a", as.character(i)), 
                       x = c(data$Latitude[i-1]-var.latitude, data$Latitude[i]-var.latitude, 
                             data$Latitude[i]+var.latitude, data$Latitude[i-1]+var.latitude), 
                       y = c(data$Longitude[i-1], data$Longitude[i], data$Longitude[i], data$Longitude[i-1]))
  pos.poly = rbind(pos.poly, loc.pos1)
  loc.pos2 = data.frame(id = paste0("b", as.character(i)), 
                        x = c(data$Latitude[i-1], data$Latitude[i], data$Latitude[i], data$Latitude[i-1]), 
                        y = c(data$Longitude[i-1]+var.longitude, data$Longitude[i]+var.longitude, 
                              data$Longitude[i]-var.longitude, data$Longitude[i-1]-var.longitude))
  pos.poly = rbind(pos.poly, loc.pos2)
  loc.pos3 = data.frame(id = paste0("c", as.character(i)), 
                        x = c(data$Latitude[i]-var.latitude, data$Latitude[i], data$Latitude[i]+var.latitude, data$Latitude[i]), 
                        y = c(data$Longitude[i], data$Longitude[i]+var.longitude, data$Longitude[i], data$Longitude[i]-var.longitude))
  pos.poly = rbind(pos.poly, loc.pos3)
}

This is plotted from two datasets so we need to specify data and the aes a couple more times.

plot1 = ggplot(pos.poly, aes(x=x, y=y)) + geom_polygon(aes(group=id), fill="white") + geom_path(data = data, aes(x=Latitude, y=Longitude))
plot1 = plot1 + xlab("Latitude") + ylab("Longitude") +  
  geom_errorbar(data = data, aes(x=Latitude,y=Longitude, ymin=Longitude-var.longitude, ymax=Longitude+var.longitude)) +
  geom_errorbarh(data = data, aes(xmin=Latitude-var.latitude,xmax=Latitude+var.latitude, x=Latitude, y=Longitude))
print(plot1)

enter image description here

Variance in y direction seems to be handled incorrectly, see e.g. the point with the highest longitude, or the one with the lowest longitude. It would also be good to use variable variances, to make the code handles corner cases correctly. — Claus Wilke, Jul 08 '15 at 13:55
@ClausWilke while this sure looks strange (and at first startled me as well) it seems desired behaviour to me: variance in x direction is that large and the white area corresponds to what you would get from shifting a dot with errorbars from point to point along the path. — mts, Jul 08 '15 at 14:01
@mts Yes, I think the main issue is actually fundamental to the plot: it is not entirely clear in this representation what the thickness of the white line means. Visually, we assess the thickness orthogonally to the connecting lines, but mathematically that's not how the thickness is set. To know whether this behavior is desired or not, we'd actually need a clear and unambiguous definition of what the width of the white line is actually supposed to represent. — Claus Wilke, Jul 08 '15 at 21:35
@ClausWike The width of the line is the variance in this case. — ayush, Jul 09 '15 at 04:50

How can I highlight variance over a ggplot?

1 Answers1

Linked