random permutation

Question

I would like to genrate a random permutation as fast as possible. The problem: The knuth shuffle which is O(n) involves generating n random numbers. Since generating random numbers is quite expensive. I would like to find an O(n) function involving a fixed O(1) amount of random numbers.

I realize that this question has been asked before, but I did not see any relevant answers.

Just to stress a point: I am not looking for anything less than O(n), just an algorithm involving less generation of random numbers.

Thanks

Answer 1

Create a 1-1 mapping of each permutation to a number from 1 to n! (n factorial). Generate a random number in 1 to n!, use the mapping, get the permutation.

For the mapping, perhaps this will be useful: http://en.wikipedia.org/wiki/Permutation#Numbering_permutations

Of course, this would get out of hand quickly, as n! can become really large soon.

Answer 2

Generating a random number takes long time you say? The implementation of Javas Random.nextInt is roughly

oldseed = seed;
nextseed = (oldseed * multiplier + addend) & mask;
return (int)(nextseed >>> (48 - bits));

Is that too much work to do for each element?

Answer 3

See https://doi.org/10.1145/3009909 for a careful analysis of the number of random bits required to generate a random permutation. (It's open-access, but it's not easy reading! Bottom line: if carefully implemented, all of the usual methods for generating random permutations are efficient in their use of random bits.)

And... if your goal is to generate a random permutation rapidly for large N, I'd suggest you try the MergeShuffle algorithm. An article published in 2015 claimed a factor-of-two speedup over Fisher-Yates in both parallel and sequential implementations, and a significant speedup in sequential computations over the other standard algorithm they tested (Rao-Sandelius).

An implementation of MergeShuffle (and of the usual Fisher-Yates and Rao-Sandelius algorithms) is available at https://github.com/axel-bacher/mergeshuffle. But caveat emptor! The authors are theoreticians, not software engineers. They have published their experimental code to github but aren't maintaining it. Someday, I imagine someone (perhaps you!) will add MergeShuffle to GSL. At present gsl_ran_shuffle() is an implementation of Fisher-Yates, see https://www.gnu.org/software/gsl/doc/html/randist.html?highlight=gsl_ran_shuffle.

Answer 4

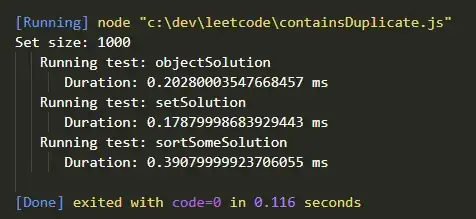
Are you sure that your mathematical and algorithmical approach to the problem is correct?

I hit exactly same problem where Fisher–Yates shuffle will be bottleneck in corner cases. But for me the real problem is brute force algorithm that doesn't scale well to all problems. Following story explains the problem and optimizations that I have come up with so far.

Dealing cards for 4 players

Number of possible deals is 96 bit number. That puts quite a stress for random number generator to avoid statical anomalies when selecting play plan from generated sample set of deals. I choose to use 2xmt19937_64 seeded from /dev/random because of the long period and heavy advertisement in web that it is good for scientific simulations.

Simple approach is to use Fisher–Yates shuffle to generate deals and filter out deals that don't match already collected information. Knuth shuffle takes ~1400 CPU cycles per deal mostly because I have to generate 51 random numbers and swap 51 times entries in the table.

That doesn't matter for normal cases where I would only need to generate 10000-100000 deals in 7 minutes. But there is extreme cases when filters may select only very small subset of hands requiring huge number of deals to be generated.

Using single number for multiple cards

When profiling with callgrind (valgrind) I noticed that main slow down was C++ random number generator (after switching away from std::uniform_int_distribution that was first bottleneck).

Then I came up with idea that I can use single random number for multiple cards. The idea is to use least significant information from the number first and then erase that information.

int number = uniform_rng(0, 52*51*50*49);
int card1 = number % 52;
number /= 52;
int cards2 = number % 51;
number /= 51;
......

Of course that is only minor optimization because generation is still O(N).

Generation using bit permutations

Next idea was exactly solution asked in here but I ended up still with O(N) but with larger cost than original shuffle. But lets look into solution and why it fails so miserably.

I decided to use idea Dealing All the Deals by John Christman

void Deal::generate()
{
    // 52:26 split, 52!/(26!)**2 = 495,918,532,948,1041
    max = 495918532948104LU;
    partner = uniform_rng(eng1, max);

    // 2x 26:13 splits, (26!)**2/(13!)**2 = 10,400,600**2
    max = 10400600LU*10400600LU;
    hands = uniform_rng(eng2, max);

    // Create 104 bit presentation of deal (2 bits per card)
    select_deal(id, partner, hands);
}

So far good and pretty good looking but select_deal implementation is PITA.

void select_deal(Id &new_id, uint64_t partner, uint64_t hands)
{
    unsigned idx;
    unsigned e, n, ns = 26;

    e = n = 13;

    // Figure out partnership who owns which card
    for (idx = CARDS_IN_SUIT*NUM_SUITS; idx > 0; ) {
        uint64_t cut = ncr(idx - 1, ns);

        if (partner >= cut) {
            partner -= cut;
            // Figure out if N or S holds the card
            ns--;
            cut = ncr(ns, n) * 10400600LU;

            if (hands > cut) {
                hands -= cut;
                n--;
            } else
                new_id[idx%NUM_SUITS] |= 1 << (idx/NUM_SUITS);

        } else
            new_id[idx%NUM_SUITS + NUM_SUITS] |= 1 << (idx/NUM_SUITS);

        idx--;
    }

    unsigned ew = 26;
    // Figure out if E or W holds a card
    for (idx = CARDS_IN_SUIT*NUM_SUITS; idx-- > 0; ) {
        if (new_id[idx%NUM_SUITS + NUM_SUITS] & (1 << (idx/NUM_SUITS))) {
            uint64_t cut = ncr(--ew, e);

            if (hands >= cut) {
                hands -= cut;
                e--;
            } else
                new_id[idx%NUM_SUITS] |= 1 << (idx/NUM_SUITS);

        }
    }
}

Now that I had the O(N) permutation solution done to prove algorithm could work I started searching for O(1) mapping from random number to bit permutation. Too bad it looks like only solution would be using huge lookup tables that would kill CPU caches. That doesn't sound good idea for AI that will be using very large amount of caches for double dummy analyzer.

Mathematical solution

After all hard work to figure out how to generate random bit permutations I decided go back to maths. It is entirely possible to apply filters before dealing cards. That requires splitting deals to manageable number of layered sets and selecting between sets based on their relative probabilities after filtering out impossible sets.

I don't yet have code ready for that to tests how much cycles I'm wasting in common case where filter is selecting major part of deal. But I believe this approach gives the most stable generation performance keeping the cost less than 0.1%.

Answer 5

Not what you asked exactly, but if provided random number generator doesn't satisfy you, may be you should try something different. Generally, pseudorandom number generation can be very simple.

Probably, best-known algorithm
http://en.wikipedia.org/wiki/Linear_congruential_generator

More
http://en.wikipedia.org/wiki/List_of_pseudorandom_number_generators

Answer 6

As other answers suggest, you can make a random integer in the range 0 to N! and use it to produce a shuffle. Although theoretically correct, this won't be faster in general since N! grows fast and you'll spend all your time doing bigint arithmetic.

If you want speed and you don't mind trading off some randomness, you will be much better off using a less good random number generator. A linear congruential generator (see http://en.wikipedia.org/wiki/Linear_congruential_generator) will give you a random number in a few cycles.

Answer 7

Usually there is no need in full-range of next random value, so to use exactly the same amount of randomness you can use next approach (which is almost like random(0,N!), I guess):

// ...
m = 1; // range of random buffer (single variant)
r = 0; // random buffer (number zero)
// ... 
for(/* ... */) {
    while (m < n) { // range of our buffer is too narrow for "n"
        r = r*RAND_MAX + random(); // add another random to our random-buffer
        m *= RAND_MAX; // update range of random-buffer
    }
    x = r % n; // pull-out  next random with range "n"
    r /= n; // remove it from random-buffer
    m /= n; // fix range of random-buffer
    // ...
}

P.S. of course there will be some errors related with division by value different from 2^n, but they will be distributed among resulted samples.

Answer 8

Generate N numbers (N < of the number of random number you need) before to do the computation, or store them in an array as data, with your slow but good random generator; then pick up a number simply incrementing an index into the array inside your computing loop; if you need different seeds, create multiple tables.

Answer 9

Generate a 32 bit integer. For each index i (maybe only up to half the number of elements in the array), if bit i % 32 is 1, swap i with n - i - 1.

Of course, this might not be random enough for your purposes. You could probably improve this by not swapping with n - i - 1, but rather by another function applied to n and i that gives better distribution. You could even use two functions: one for when the bit is 0 and another for when it's 1.