Wagner–Fischer algorithm

Question

I'm trying to understand the Wagner–Fischer algorithm for finding distance between to strings. I'm looking through a pseudocode of it in the following link: http://en.wikipedia.org/wiki/Wagner%E2%80%93Fischer_algorithm

int EditDistance(char s[1..m], char t[1..n])
   // For all i and j, d[i,j] will hold the Levenshtein distance between
   // the first i characters of s and the first j characters of t.
   // Note that d has (m+1)  x(n+1) values.
   let d be a 2-d array of int with dimensions [0..m, 0..n]

   for i in [0..m]
     d[i, 0] ← i // the distance of any first string to an empty second string
   for j in [0..n]
     d[0, j] ← j // the distance of any second string to an empty first string

   for j in [1..n]
     for i in [1..m]
       if s[i] = t[j] then  
         d[i, j] ← d[i-1, j-1]       // no operation required
       else
         d[i, j] ← minimum of
                    (
                      d[i-1, j] + 1,  // a deletion
                      d[i, j-1] + 1,  // an insertion
                      d[i-1, j-1] + 1 // a substitution
                    )

   return d[m,n]

Actually I get the algorithm's point and understand it intuitively, by it's not obvious for me why are d[i-1, j] + 1, d[i, j-1] + 1 and d[i-1, j-1] + 1 considered as a deletion, insertion and substitution. It'd be great if someone explained the implementation nuances in a more detailed way.

Answer 1

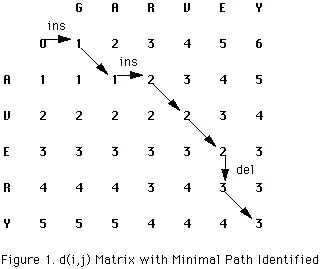
I have created a gist which prints out the sequence of operations as well as the goal which each step is trying to solve, which should complement my explanation of the Fischer-Wagner algorithm.

To be able to understand the Fischer-Wagner algorithm you have to keep in mind that it is belongs to the family of dynamic programming algorithms. This means that it will compute partial solutions to a bigger problem, store the partial solution and use the result of the partial computation for the next computation.

So what does this mean for the Fisher-Wagner algorithm? In this context this means that each element of the distance matrix d contains the best possible trace of operations to get you from your current string A to another string B. This explanation is still a little bit abstract, so let me explain what I mean by that by walking you through an example.

Lets assume you want to calculate the Levensthein distance of the two strings "ABV" and "FV" using the Fischer-Wagner algorithm. Then your distance matrix will look like this:

+-----+---+---+---+---+
|     |j->| 0 | 1 | 2 |
+-----+---+---+---+---+
|   i |   | # | F | V |
+-----+---+---+---+---+
|   0 | # |   |   |   |
|   1 | A |   |   |   |
|   2 | B |   |   |   |
|   3 | C |   |   |   |
+-----+---+---+---+---+

The first row/column of this table name the indices of the distance matrix, the second name the characters of the strings. '#' is the empty string (i.e. a string with zero length).

Each element of this distance matrix marks a subproblems that you want to solve. For example, the entry [i=0, j=2] contains the shortest distance from arriving from an empty string "" to "FV" the entry [i=2, j=1] contains the shortest distance for the problem "AB" => "F".

Let's fast forward the algorithm to the subproblem [i=2, j=2], i.e. how to get from "AB" to "FV". In this case, the distance matrix looks like this.

+-----+---+---+---+---+
|     |j->| 0 | 1 | 2 |
+-----+---+---+---+---+
|   i |   | # | F | V |
+-----+---+---+---+---+
|   0 | # | 0 | 1 | 2 |
|   1 | A | 1 | 1 | 2 |
|   2 | B | 2 | 2 |   |
|   3 | C | 3 | 3 |   |
+-----+---+---+---+---+ 

"B" and "V" are not equal, which means we need to perform one of the following three operations to make them equal:

1. delete "B". We take the cost of the cell above d[i=1, j=2], because we know that this cell is the cheapest sequence of operations that gets us from "A" => "FV". However, our problem is getting from "AB" => "FV", not from "A" => "FV. We do know that we can replace "A" by "FV" by applying the operations of cell d[i=1, j=2] (we solved this subproblem earlier), which leaves us with a string "FVB" for the cost of 2. We then deleted the "B" ("FVB" => "FV") and we are done. The cost of this operation is 2+1.
2. insert "V". Similar as delete "B", only we take the value to the left d[i=2, j=1] because we know it is the cheapest sequence of operations to get from "AB"=>"F". Since our problem is to get from "AB"=>"FV", we only need to add the cost of inserting "V" and we are done.
3. substitute "B" with "V". Similar to the previous cases. We know that d[i=1, j=1] contains the cheapest sequence of operations to change "A"=>"F". Applying this operation changes our problem changes to "FB"=>"FV", which can be solve by substituting "B" with "F".

After considering these 3 options, we pick the cheapest one, which is substituting "B" by "F" (1+1).

After solving all subproblems in that fashion, the output will produce the final result, which is the minimal edit distance from "ABC => "FV".

Answer 2

Note the string which is imagined to be kept at columns is constant and we need to find the edit distance of the string kept at rows . See this for example

Here we are trying to compute Edit distance of AVERY ! So now, the substructure DP[i][j]=DP[i-1][j-1] (if G[j]==A[i])

NOTE: G stands for GARVEY and A for AVERY

because If we can solve Edit Distance of G[j-1] and A[i-1] in k operations we can solve G[j] and A[i] operations ( No operation needed for last character)

Other wise

DP[i][j]= minimum of following

DP[i-1][j]+1 (See we can only delete from the Row String (whose EDIT distance is to be calculated !) DP[i-1][j] represents the string G[1...j] and A[1...i-1]! See the character A[i] deleted??)

DP[i][j-1]+1 (See this is not a deletion!! What we do is add a character at i+1 th posiition ! And hence it is equal to G[j] (We can add any character))

DP[i-1][j-1]+1 (I guess this is easy now the i th and j th character weren't same so what we did was change the A[i] th character into G[j]th)

Feel free to ask doubts :)

Answer 3

Here is a very clear article. The memoized recursive version may be easier to understand, the difference is that the subproblems are evaluated in a different order.