I have a (world) matrix, and it applies translation, rotation and scale into an 3D object. It is created with the function XMMatrixTransformation (DirectXMath) and the parameter RotationQuaternion is made by a call to XMQuaternionRotationRollPitchYaw. Then it is stored in a file along with other data.
Then I need to recover the values, so I can use this function to decompose it to each component:
XMMatrixDecompose(&Scale, &RotationQ, &Translation, Matrix);
Scale and translation are vectors and rotation is a quaternion. If the matrix rotates the object in a single axis I could use this to convert the quaternion back to the angles:
XMQuaternionToAxisAngle(&Axis, &Angle, RotationQ);
It works fine. But when it rotates in two or more axes how can I do the same? Is there a way to do that?
PS: I don't care if the output angles aren't the same as the input. They just need to be equivalent.
PS2: Okay, so I followed Gene's link (I had already looked there but didn't found what I needed that time). I made this code based in this equation I found in Wikipedia:
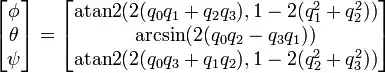
float Roll = atan2(2.0*(F.x*F.y + F.z*F.w), 1 - 2 * (F.y*F.y + F.z*F.z));
float Pitch = asin(2.0*(F.x*F.z - F.w*F.y));
float Yaw = atan2(2.0*(F.x*F.w + F.y*F.z), 1 - 2 * (F.y*F.y + F.z*F.z));
In the output I have different angles. The output seems to be equivalent for (90°, 0°, 90°), but not for (45°, 45°, 45°).