I have several weighted values for which I am taking a weighted average. I want to calculate a weighted standard deviation using the weighted values and weighted average. How would I modify the typical standard deviation to include weights on each measurement?
This is the standard deviation formula I am using.

When I simply use each weighted value for 'x' and the weighted average for '\bar{x}', the result seems smaller than it should be.
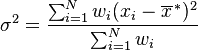 ,
,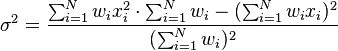 .
.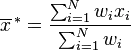 .
.