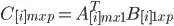There's a way to multiply 2 IndexedRowMatrix using the RDDs, but you need to write it by yourself. Notice that in the implementation that I'm showing you get a DenseMatrix as result.
Background
Let's assume you have 2 matrices Amxn and Bnxp, and you want to compute Amxn * Bnxp = Cmxp (typically n >> m and n >> p, otherwise you wouldn't be using IndexRowMatrices)
An A(i)mx1 is the i column vector of Amxn and it's stored in a row of IndexedRowMatrix. Similarly, B(i)1xp is the i row vector stored in a row of the correspondent IndexedRowMatrix.
Also it's not difficult to prove that 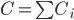 such that
such that
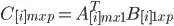
These two operations described above can be easily implemented in a map+reduce operation, or more efficiently in a .treeAggregate when nxp is big.
Version 1: Using Breeze
Simple implementation using Breeze Matrices to perform the multiplications, assuming your matrices are dense (if not you can do some further optimizations).
import breeze.linalg.{DenseMatrix => BDM}
def distributedMul(a: IndexedRowMatrix, b: IndexedRowMatrix, m: Int, p: Int): Matrix = {
val aRows = a.rows.map((iV) => (iV.index, iV.vector))
val bRows = b.rows.map((iV) => (iV.index, iV.vector))
val joint = aRows.join(bRows)
def vectorMul(e: (Long, (Vector, Vector))): BDM[Double] = {
val v1 = BDM.create(rows, 1, e._2._1.toArray)
val v2 = BDM.create[Double](1, cols, e._2._2.toArray)
v1 * v2 // This is C(i)
}
Matrices.dense(m, p, joint.map(vectorMul).reduce(_ + _).toArray)
}
Notes
- numRows(), numCols() on IndexedRowMatrix can be costly. If you know the dimensions you can provide them right away as arguments
- Instead of a join you can use a cartesian, however you need to add an if and return zero matrix when indexes are different
Version 2: Using BLAS
This version is more efficient than the other (there is another version using only Scala arrays but it's extremely inefficient). You need to place it in an object because BLAS is not serializable.
import com.github.fommil.netlib.BLAS
object SuperMul extends Serializable{
val blas = BLAS.getInstance()
def distributedMul(a: IndexedRowMatrix, b: IndexedRowMatrix, m: Int, p: Int): Matrix = {
val aRows = a.rows.map((iV) => (iV.index, iV.vector))
val bRows = b.rows.map((iV) => (iV.index, iV.vector))
val joint = aRows.join(bRows)
val dim = m * p
def summul(u: Array[Double], e: (Long, (Vector, Vector))): Array[Double] = {
// u = a'(i)*b(i) + u
blas.dgemm("N", "T", m, p, 1, 1.0, e._2._1.toArray, m, e._2._2.toArray, p, 1.0, u, m)
u
}
def sum(u: Array[Double], v: Array[Double]): Array[Double] = {
blas.daxpy(dim, 1.0, u, 1, v, 1)
v
}
Matrices.dense(m, p, joint.treeAggregate(Array.fill[Double](dim)(0))(summul, sum))
}
}
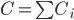 such that
such that