4

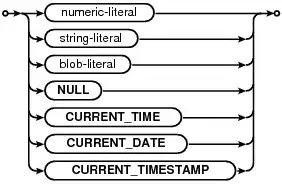
I must do some calculations that need to use trigonometric functions, and especially the atan one. The code will run on an Atmega328p, and for efficiency sake, I can't use floats: I'm using fixed point numbers. Thus, I can't use the standard atan function.

I which to have a function which take a value in fixed point format s16_10 (signed, 16 bits width, point in 10th position), and returns a s16_6 format. The input will be between 0 and 1 (so 0 and 210), so the output, in degrees, will be between -45 and 45 (so -45 * 26 and 45 * 26).

Let's say that Y is the fixed point, s16_6 representation of y, the real angle of the arc, and x such as atan(x) = y, and X the s16_10 representation of x. I start with approximating the atan function, from (0,1) to (-45,45) with a 4th degrees polynomial, and found that we can use:

y ~= 8.11 * x^4 - 19.67 * x^3 - 0.93 * x^2 + 57.52 * x + 0.0096

Which leads to:

Y ~= (8.11 * X^4)/2^34 - (19.62* X^3)/2^24 - (0.93 * X^2)/2^14 + (57.52*X)/2^4 + 0.0069 * 2^6

And here am I stuck... On the one hand, computing the X^4 will lead to a 0 for one fifth of the definition interval, and on the other and the 2n4n in {3, 2, 1} will often lead also to a zero value... How could I do ?

Spirine
  • 1,837
  • 1
  • 16
  • 28
  • 1
    There probably is a typo in the last sentence ("and on the other and the 2n4 will often lead also") - please clarify. Also, when some intermediate result is 0, why is that a problem? – anatolyg May 14 '15 at 17:21
  • 1
    Also, are you obliged to use Taylor series? There is [CORDIC](http://en.wikipedia.org/wiki/CORDIC) which may be more efficient; I have never heard about Atmega328p so cannot determine which algorithm is better. – anatolyg May 14 '15 at 17:25
  • @anatolyg I've edited the answer for clarity! It's a problem in so far as the three first members are always zero... And I can't find an approximation which doesn't nullify the variable. I didn't know it was a Taylor serie, but I'll look CORDIC algorithm – Spirine May 14 '15 at 17:41
  • Are you using `_Accum` or a custom type? – Ignacio Vazquez-Abrams May 14 '15 at 18:37
  • 1
    I'm using `typedef int16_t fixed16_p` where p is the position of the point – Spirine May 14 '15 at 19:14
  • For the x^4 term, you could introduce `sqrt(8.11)` as the multiplier between the first and second squaring. – Sneftel May 15 '15 at 00:26
  • @anatolyg This isn't Taylor series of atan, it's a result of curve-fitting to atan with a polynomial. –  May 15 '15 at 00:26
  • It might be useful to know that atan(x) = (pi/2) - atan(1 / x). If your function is more accurate when abs(x) < 1 then you can take the inverse when it is > 1 and then subtract the result from (pi/2), or vice versa if abs(x) > 1 is more accurate. Limiting the input range to -1 to 1 might also enable you to use a lookup table – samgak May 15 '15 at 03:20

1 Answers1

5

Some of the terms being truncated to zero is not necessarily a disaster; this doesn't substantially worsen your approximation. I simulated your fixed precision setup in Matlab by rounding each term of the polynomial to the nearest integer: 

q4 = @(X) round((8.11 * X.^4)/2^34);
q3 = @(X) -round((19.62* X.^3)/2^24);
q2 = @(X) -round((0.93 * X.^2)/2^14);
q1 = @(X) round((57.52*X)/2^4);
q0 = @(X) round(0.0069 * 2^6);

It's true that on the first fifth of the interval [0,210] the terms q4, q3, q2 look rather choppy, and q4 is essentially absent.

terms

But these effects of rounding are of about the same size as the theoretical error of approximation of atan by your polynomial. Here is the plot where red is the difference (polynomial-atan) calculated without rounding to integers, and green is the difference (q4+q3+q2+q1+q0-atan):

atanapprox

As you can see, rounding does not make approximation much worse; in most cases it actually reduces the error by a happy accident.

I do notice that your polynomial systematically overestimates atan. When I fit a 4th degree polynomial to atan on [0,1] with Matlab, the coefficients are slightly different: 

8.0927  -19.6568   -0.9257   57.5106   -0.0083

Even truncating these to two significant figures, as you did, I get a better approximation: 

(8.09 * X^4)/2^34 - (19.66* X^3)/2^24 - (0.93 * X^2)/2^14 + (57.52*X)/2^4 - 0.0083 * 2^6

betterpoly

This time the truncation to integers does worsen things. But it is to be expected that the outcome of a calculation where several intermediate results are rounded to integers will be off by +-2 or so. The theoretical accuracy of +-0.5, shown by this polynomial, cannot be realized with the given arithmetical tools.