6

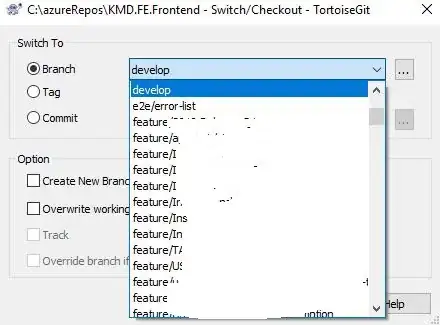
Using the recent version of sympy (0.7.6) I get the following bad result when determining the integral of a function with support [0,y):

from sympy import *
a,b,c,x,z = symbols("a,b,c,x,z",real = True)
y = Symbol("y",real=True,positive=True)
inner = Piecewise((0,(x>=y)|(x<0)|(b>c)),(a,True))
I = Integral(inner,(x,0,z))
Eq(I,I.doit())

This is incorrect as the actual result should have the last two cases swapped. This can be confirmed by checking the derivative:

Derivative(I.doit(),z).doit().simplify().subs(z,x)

which reduces to 0 everywhere.

Interestingly, when dropping the condition (b>c) by substituting inner = Piecewise((0,(x>=y)|(x<0)),(a,True)) I get a TypeError:

TypeError: cannot determine truth value of
-oo < y

Am I using the library incorrectly or is this actually a serious sympy bug?

Glorfindel
  • 21,988
  • 13
  • 81
  • 109
Lars Melchior
  • 292
  • 1
  • 9

1 Answers1

4

Yes, sympy 0.7.6 is wrong in this case, and in some other such cases. Generally, I don't know any symbolic math package that I would trust to do calculus with piecewise defined functions.

Note that although 

inner = Piecewise((0, (x>=y)|(x<0)), (a,True))

throws a TypeError at integration time, a logically equivalent definition 

inner = Piecewise((a, (x<y)&(x>=0)), (0,True))

leads to the correct result

Piecewise((a*z, And(z < y, z >= 0)), (0, And(z <= 0, z >= -oo)), (a*y, True))

By the way, the previous version, sympy 0.7.5, handles

inner = Piecewise( (0, (x>=y)|(x<0)), (a,True) )

without a TypeError, producing the correct result (in a different form):

Piecewise((0, z <= 0), (a*y, z >= y), (a*z, True))

Here is another, simpler example of buggy behavior: 

>>> Integral(Piecewise((1,(x<1)|(z<x)), (0,True)) ,(x,0,2)).doit()
-Max(0, Min(2, Max(0, z))) + 3

>>> Integral(Piecewise((1,(x<1)|(x>z)), (0,True)) ,(x,0,2)).doit()
-Max(0, Min(2, Max(1, z))) + 3

The first result is incorrect (it fails for z=0, for example). The second is correct. The only difference between two formulas is z<x vs x>z.

  • Thanks, that confirms my suspicion. Any insight as to why symbolic math packages struggle so much with piecewise defined functions? I would believe that its just a matter of splitting the integral and choosing the right integration limits. Shouldn't sympy raise a NotImplementedError on piecewise functions if this is known buggy behavior? – Lars Melchior May 14 '15 at 07:33
  • I don't know sympy internals. I just know empirically that CAS struggle with such things, for example [Wolfram Alpha](http://www.wolframalpha.com/input/?i=integral+abs%28sin%28x%29%29) gets the indefinite integral of |sin x| wrong. If you have access to Maple or Mathematica (I don't at present), you may want to compare the result with theirs. –  May 14 '15 at 16:10
  • Actually, the result I'm getting from wolfram alpha is -cos(x)sign(sin(x)) + c , which is the correct antiderivative (note that in the definite case c has to increase by 2 for every half-period). – Lars Melchior May 15 '15 at 09:12
  • If something increases by 2, it is not a constant anymore. In any case, WA did not tell you about this increase, you had to find it on your own. If you simply took its answer and used in calculations without rechecking, the result would be wrong. –  May 15 '15 at 13:51
  • The [wolfram documentation for indefinite integrals](http://mathworld.wolfram.com/IndefiniteIntegral.html) states that c is only a piecewise constant function. Either way, the antiderivative is correct. To determine the definite integral, you must use the [First Fundamental Theorem of Calculus](http://mathworld.wolfram.com/FirstFundamentalTheoremofCalculus.html) which only works on continuous functions, so you have to choose this piecewise constant accordingly. I agree that this should have been made clearer by WA, however it seems to me that they have no problem with piecewise functions. – Lars Melchior May 15 '15 at 14:18
  • A closer comparison to your question would be [integral abs(sin(x)) from 0 to z](http://www.wolframalpha.com/input/?i=integral+abs%28sin%28x%29%29+from+0+to+z) which WA returns unevaluated. –  May 15 '15 at 14:21
  • That is True. Numeric limits do work though, and at least the result is not incorrect. Btw I've linked to here from a [similar sympy issue](https://github.com/sympy/sympy/issues/8919). lets see if this gets fixed. – Lars Melchior May 15 '15 at 14:34