Grammar which generate language a^i^2?

Question

Can anybode show what production rules are needed for constructing grammar for language

a^i^2 where ^ means power of

Can it be described by a grammar?

EDIT:

This is similar but kind of "weaker" grammar since you are not doing powers but multiples of 2.

enter image description here

It is context-sensitive grammar, I didn't write down all the rules, but idea is of the form:

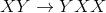
enter image description here

You multiply X's with Y and then delete Y on the left side. I thought that maybe with powers you can generate Y's going to right, and then generate final X's going back right but I think that doesn't really work.

Do you have any ideas?

At least it can not be described by a context-free grammar (and therefore not by a regular grammar), because it does not satisfy pumping lemma. For a unrestricted grammar, I can't say. — Petr, May 03 '15 at 11:42
@Petr I added example why it should be context-sensitive or "stronger" — martinerk0, May 03 '15 at 12:15

Petr · Answer 1 · 2015-05-03T12:55:28.357

1

I've found the following answer here: http://www.mersenneforum.org/showthread.php?t=11676

S→LAYR 
ZA→aAZ 
Za→aZ
ZR→AAYR 
aY→Ya 
AY→YA 
LY→LZ 
YR→X 
aX→Xa 
AX→Xa 
LX→ε 
Since n^2 =\sum_{i=1}^{n} (2i-1), at any instance, for n=i, we have (i-1)^2 A's and (2i-1) a's. For n=i+1, all the A's are converted into a's, and goes ahead.

Though I have not verified it completely.

edited May 03 '15 at 12:55

answered May 03 '15 at 12:39

Petr

9,812
1
28
52

Grammar which generate language a^i^2?

1 Answers1