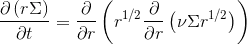This may be a simple question but what is the correct FiPy syntax to use if I want to solve PDE with spatially varying coefficient that is outside of gradient? All the examples I've seen so far only talk about coefficient inside of the gradient.
For example:
d/dt(Sigma) = (1/r) d/dr (r^0.5 d/dr(nu Sigma r^0.5))
(I'm ignoring numerical factors)
and I want to solve for Sigma(t,r). How do I handle (1/r) in front of d/dr?
I know this simple equation can be massaged so that I don't need to worry about spatially varying coefficient that is outside of gradient (or simply move the coefficient inside the time derivative term) but I'll have to add in more terms for the actual problem I'm trying to solve and the trick will no longer be valid. For instance, what should I do if my equation looks like:
d/dt (var) = f(r) d^2/dr^2 (var) + g(r) d/dr (var)
Any help would be greatly appreciated!