solving nonlinear equations in matlab

Question

I have a homework question that I cannot answer. Here is the question prompt:

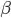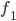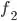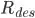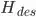Deﬁne Eq. 8.3 and Eq. 8.4 in a function. This function should take a vector of joint angles ( $\alpha$ and $\beta$ ) as input and should return a column vector containing the two functions ( $f_{1}$ and $f_{2}$ ) evaluated at those angles. The function should contain the link lengths and values of and $H_{des} = 1.1$ for calculation. Include your code in your solution.

Equations 8.3 and 8.4 are:

formula (8.3)

formula (8.4)

where

$d_{1} = d_{2} = 1.0$

R{des} = 1

$H_{des} = 1.1$

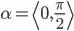
$\alpha = \left \langle 0, \frac{\pi}{2} \right \rangle$

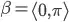
$\beta = \left \langle 0, \pi \right \rangle$

Here is the function I wrote:

function F = rob_arm (alphag, betag)
F = (1).*cos(alphag)+ (1).*(cos(alphag+betag))-(1) ;
  (1).*sin(alphag) + (1).*(sin(alphag+betag))-(1.1) ;
end

Because alpha and beta are matrices of different sizes, I used meshgrid to create alphag and betag, and used those matrices to calculate the values of rob_arm. After four hours of messing with this, I'm not even sure what the question is asking anymore, and the TA's are not currently answering emails. I wrote the following code, to try and force rob_arm into a single column:

alpha = 0:pi/100:(pi/2); %define angle alpha
beta = 0:pi/100:pi; %define angle beta

[alphag, betag] = meshgrid (alpha, beta); %mesh grid alpha and beta b/c different matrix dimensions
arm_pos = rob_arm (alphag, betag);

for ii = 1:1:101
    for k = 1:1:51
 col_vec (1,1:1:5151) = arm_pos(ii,k);
    end
end

Ignoring the query to create a column vector, the resulting output, arm_pos is good output. I can graph it and I get a very pretty picture of all the possible points that this robot arm can 'reach.'

But because I am dumb and have been trying this for many hours, it's not saving successive values of rob_arm into col_vec, it just replaces it each time and I end up with a 1x1 matrix. Ultimately, the goal will be to use the Newton-Raphson method to determine the zeroes of this function, but that's a long ways off. I am thinking if I can get all of the values calculated by rob_arm into a single column, then I can answer this question.

The next question is:

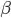Create a separate function that accepts input of a single row vector containing the pair of angles $\alpha$ and $\beta$ . The output of the function should be the Jacobian (a 2 by 2 matrix). First, calculate the derivatives of Eqs. 8.3 – 8.4 by hand, then put them into your function. Include your function code in your solution

Which I will need to ask for clarification on, because I don't understand how a 1 x 51 matrix (alpha) and a 1 x 102 matrix (beta) could be accepted into a single row vector, that would then output a 2x2 matrix. I know what the Jacobian is, and it is the partial derivitives of my two functions, not a matrix of values.

If anyone wants to give me a hand, that would be super awesome.

Isn't this as simple to correct as returning the function value as a vector, `F = [ f1; f2 ]` with the corresponding expressions for `f1` and `f2`? — Lutz Lehmann, Mar 30 '15 at 08:55
To ellaborate on LutzLs comment: try `function F = rob_arm (alphag, betag) F = [(1).*cos(alphag)+ (1).*(cos(alphag+betag))-(1) ; ... (1).*sin(alphag) + (1).*(sin(alphag+betag))-(1.1)]; end` — Buck Thorn, Mar 30 '15 at 15:16
Use a set of three dots "..." if continuing a statement between lines in MATLAB (in Octave it is not always necessary to have the dots...) — Buck Thorn, Mar 30 '15 at 15:17

score 0 · Answer 1 · answered Mar 30 '15 at 15:18

You function definition is not right, you should use something like

function F = rob_arm (alphag, betag) 
 F = [(1).*cos(alphag)+ (1).*(cos(alphag+betag))-(1) ; ...   
      (1).*sin(alphag) + (1).*(sin(alphag+betag))-(1.1)]; 
end

Without the three dots " ... " MATLAB performs this calculation

 (1).*sin(alphag) + (1).*(sin(alphag+betag))-(1.1);

but does nothing with the result, and returns

  F = (1).*cos(alphag)+ (1).*(cos(alphag+betag))-(1) ;

which is not what you want, half the F values are missing.

solving nonlinear equations in matlab

1 Answers1