Inverse fourier transform

Question

I'm trying to write IFT algorithm. Here is my code:

%% Fourier Analysis
N = 20;
T1 = 0.25*N;
T0 = N;
x = [zeros(T1,1); ones(T0/2,1); zeros(T1,1)]';

omega = 2*pi*1/T0;

ak = zeros(1,2*N+1);

for k = -N:N
    if k == 0
        ak(k+N+1) = 2*T1/T0;
    else
        ak(k+N+1) = sin(k*omega*T1)/(k*pi);
    end
end

%Approximate the periodic symmetric square wave
t=linspace(-0.5,0.5,N);

for n=1:length(t)
    xN(n)=0;
    for k = -N:N
        xN(n) = xN(n) + ak(k+N+1).*exp(1i*k*omega*t(n));
    end
end

What's wrong with it (I know that Matlab have ifft() function, but I would like to write my own)? I use for it this code:

ift

The result should looks like (EN is error):

enter image description here

Where black plot is xN and blue plot is x. My result is straight line.

"What's wrong with it" - you tell us - in what way is it not doing what you expect ? — Paul R, Mar 19 '15 at 16:02
I expect result as with ifft() function. It should approximate the periodic symmetric square wave (x) by considering only a finite number of the Fourier series coefficients. — Kulis, Mar 19 '15 at 16:05
can you please do fft and ifft and plot that with respect to your solution? Because if those plots are your implementation, then it looks correct as far as what I would expect to see. — Rollen, Mar 19 '15 at 16:43
There results aren't show my implementation. I takes it from books. — Kulis, Mar 19 '15 at 16:49

eigenchris · Accepted Answer · 2015-03-19T19:08:33.297

I don't know where you got that formula in the image from, but for an N-point fourier transform of a discrete signal, you only need to sum over k from 0 to N-1 to get an exact reconstruction. N orthogonal basis functions can reconstruct any N-dimensional signal. You might be confusing the DTFT with the DFT (you want the second of these).

I also don't understand the formulas you used for the ak coefficients. You calculate them with sin and then sum them up with complex exponentials rather than sine waves.

If you want to do a discrete fourier transform (DFT) with a complex exponentials, the code should look similar to mine below. You get the ck coefficients from the inner product of the time signal x and the complex basis functions.

clear; clc;

N = 20;                                        %// number of points

x = [zeros(1,N/4),ones(1,N/2),zeros(1,N/4)];   %//time signal data
n = 0:N-1;

ck = zeros(1,N);
for k = 0:N-1                                  %//cacluate coefficients
    ck(k+1) = sum(x.*exp(-1i*2*pi*k*n/N));
end

xN = zeros(1,N);
for k = 0:N-1                                  %// add partial frequencies
    xN = xN + ck(k+1)*exp(1i*2*pi*k*n/N)/N;
end

plot(n,xN)

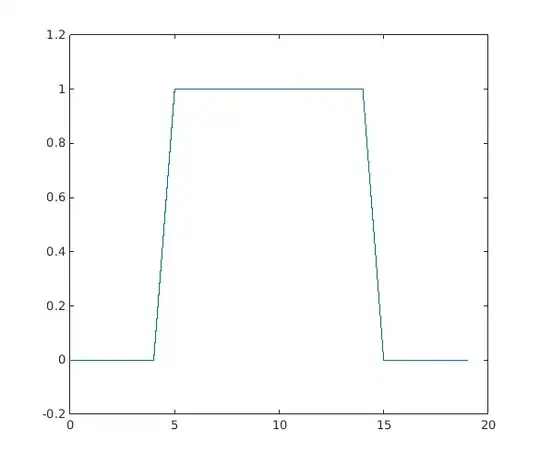
enter image description here

If you want to do an ordinary fourier series using real sinusoids, your code should look like this:

clear; clc;

N = 20;                                         %// number of points
T = 1;                                          %// fundamental frequency
omega = 2*pi/T;                                 %// angular frequency

t = linspace(-0.5,0.5,N);                       %// time points
x = [zeros(1,N/4),ones(1,N/2),zeros(1,N/4)];    %// time signal data

a0 = sum(x)/N;  ak = zeros(1,N);    bk = zeros(1,N);
for k = 1:N-1                                   %// calculate coefficients
    ak(k) = sum(x.*cos(omega*k*t))/N;
    bk(k) = sum(x.*sin(omega*k*t))/N;
end

xN = a0*cos(omega*0*t);                         %// add DC offset
for k = 1:N-1                                   %// add partial frequencies
    xN = xN + ak(k)*cos(omega*k*t) + bk(k)*sin(omega*k*t);
end

plot(t,xN)

I take it from http://s000.tinyupload.com/?file_id=47916931294804743910 (8th page). — Kulis, Mar 19 '15 at 19:35
@Kulis I see, you have the right idea in your original code, then. It seems they want you to treat `x(t)` as a real-time signal. This means you should sample `t` very finely; use far more than `N` time points, `t = linspace(-0.5,0.5,1000);`, for example. Also, set `omega = 2*pi;` since the range of our signal is `[-0.5,0.5]`, so a fundamental period of `T=1` should be used. Hopefully that gets your code working. — eigenchris, Mar 19 '15 at 20:17

Inverse fourier transform

1 Answers1