28

This is the recursive implementation of the Fibonacci sequence from Cracking the Coding Interview (5th Edition)

int fibonacci(int i) {
       if(i == 0) return 0;
       if(i == 1) return 1;
       return fibonacci(i-1) + fibonaci(i-2);
}

After watching the video on the time complexity of this algorithm, Fibonacci Time Complexity, I now understand why this algorithm runs in O(2n). However, I am struggling with analyzing the space complexity.

I looked online and had a question on this.

In this Quora thread, the author states that "In your case, you have n stack frames f(n), f(n-1), f(n-2), ..., f(1) and O(1)" . Wouldn't you have 2n stack frames? Say for f(n-2) One frame will be for the actual call f(n-2) but wouldn't there also be a call f(n-2) from f(n-1)?

funnydman
  • 9,083
  • 4
  • 40
  • 55
committedandroider
  • 8,711
  • 14
  • 71
  • 126
  • 2
    Constant factors don't matter in big-O complexity -- O(n) and O(2n) are the same. That said, stack frames are reclaimed and reused for the second call after the first call returns. – Chris Dodd Feb 27 '15 at 01:43
  • Is that LaTeX math notation, 2 to the power n ? Do you simply mean, 2 times n ? – chrisinmtown Feb 27 '15 at 01:47
  • @chrislott can you make a edit to the math jax? I mean 2 to the power n – committedandroider Feb 27 '15 at 01:52
  • @ChrisDodd so in the computer, there is one stack frame for f(n-2) and that gets used twice because there are two calls to this? – committedandroider Feb 27 '15 at 01:53
  • @committedandroider: You can edit your own posts. There is no MathJax on StackOverflow, so you have to do it with HTML. – rici Feb 27 '15 at 02:40
  • @rici is there a reference guide like [Reference MathJax](http://meta.math.stackexchange.com/questions/5020/mathjax-basic-tutorial-and-quick-reference) ? – committedandroider Feb 27 '15 at 02:42
  • @committedandroider: HTML is pathetic compared to MathJax. But it's all we have. I use and liberally, surround variables names with _ to make them italic, and memorize some entities like α and →. If you need more than that, there are services which render mathjax as png, and you can upload an image. – rici Feb 27 '15 at 02:50
  • @committedandroider: The style is described pretty well in this MetaSO answer: http://meta.stackoverflow.com/a/285924/1566221 – rici Feb 27 '15 at 02:53

5 Answers5

32

Here's a hint. Modify your code with a print statement as in the example below:

int fibonacci(int i, int stack) {
    printf("Fib: %d, %d\n", i, stack);
    if (i == 0) return 0;
    if (i == 1) return 1;
    return fibonacci(i - 1, stack + 1) + fibonacci(i - 2, stack + 1);
}

Now execute this line in main:

Fibonacci(6,1);

What's the highest value for "stack" that is printed out. You'll see that it's "6". Try other values for "i" and you'll see that the "stack" value printed never rises above the original "i" value passed in.

Since Fib(i-1) gets evaluated completely before Fib(i-2), there will never be more than i levels of recursion.

Hence, O(N).

selbie
  • 100,020
  • 15
  • 103
  • 173
  • What is the significance of that stack variable? – committedandroider Feb 27 '15 at 01:51
  • 1
    @committedandroider I usually call it `depth` instead of `stack`. It keeps track of the number of levels of recursion, so that the `printf` can display it. (You can also use it to limit the recursion depth, but that's not needed here.) – user3386109 Feb 27 '15 at 01:59
  • Is space complexity more dependent on the level of recursion or the number of stack frames? – committedandroider Feb 27 '15 at 02:03
  • 5
    @committedandroider There is one stack frame for each level of recursion, so the **space used** is equal to "the deepest level of recursion" multiplied by "the size of the stack frame for each level". The **space complexity** is just "the deepest level of recursion" since the stack frame size per level is a constant multiplier, and therefore ignored in complexity analysis. – user3386109 Feb 27 '15 at 02:10
  • So if we look at a simpler example, say f(4,1), I noticed that two f calls, f(3,2) and f(2,2) are at the same recursion level. Does that mean they use the same stack frame? – committedandroider Feb 27 '15 at 02:25
  • 1
    @committedandroider Yes and no. The `f(3,2)` instance will set up a stack frame. After `f(3,2)` returns that stack memory is reclaimed. The call to `f(2,2)` will set up a different stack frame at the same location in memory. So whether they use the same stack frame depends on how you define "same stack frame". – user3386109 Feb 27 '15 at 04:47
  • Will the eventual call to f(1,4) also set up a different stack frame at the same location in memory? – committedandroider Feb 27 '15 at 17:42
  • @committedandroider - For this simple example in a C program, yes. I actually do not know if Java's implementation of a stack frame is the same as it is for C. My intuition says yes, but that's a guess. – selbie Feb 27 '15 at 23:57
25

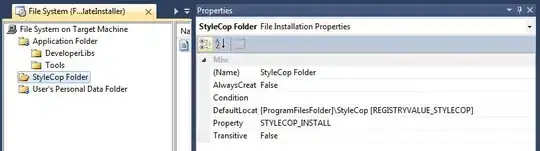
The recursive implementation has an approximative time complexity of 2 square n (2^n) which means that the algorithm will have to go approximately through 64 computing steps to get the 6th Fibonacci number. This is huge and not optimal, it will take approximately the program 1073741824 computing steps to get the Fibonacci number of 30, a small number, which is unacceptable. Practically, the iterative approach is definitely way better and optimized.

recursive fibonacci calls tree

After knowing the time complexity of this implementation, one may think that the space complexity of it may be the same and yet it is not. The space complexity of this implementation equals O(n), and it never exceeds it. So, let's demystify the "why"?.

This is because the function calls that are being executed recursively may seem, at first glance, being executed concurrently, but In reality, they are instead being executed sequentially.

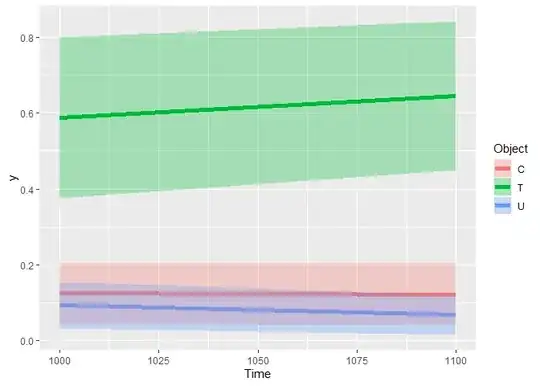
Sequential execution guarantees that the stack size will never exceed the depth of the calls' tree illustrated above. The program starts by executing all the left-most calls before turning to the right and when an F0 or F1 call return, their corresponding stack frames get popped off.

In the figure below, each rectangle represent a function call and the arrows represent the path taken by the program to reach the end of recursion:

enter image description here

What we can notice here is that when the program reaches the call F4F3F2F1 and returns 1, it goes back to its parent call F4F3F2 to execute the right recursive sub-call F4F3F2F0 and when both F4F3F2F0 and F4F3F2F1 calls return, the program returns to F4F3. So the stack never exceeds the size of the longest path F4F3F2F1.

The program will follow this same pattern of execution, going from parents to children and returning to parents after executing left and right calls until it reaches the last root parent of all F4, bringing the calculated sum of Fibonacci which 3.

isqo
  • 386
  • 4
  • 7
2

As I see it, the process would only descend one of the recursions at a time. The first (f(i-1)) will create N stack frames, the other (f(i-2)) will create N/2. So the largest is N. The other recursion branch would not use more space.

So I'd say the space complexity is N.

It is the fact that only one recursion is evaluated at a time that allows the f(i-2) to be ignored since it is smaller than the f(i-1) space.

Richard
  • 52
  • 3
  • oh is it because the other f(i-2) will wait for the first f(i-1) to finish? – committedandroider Feb 27 '15 at 02:07
  • @committedandroider. Yes, at each level all the f(i-1)'s get executed before the f(i-2)'s get started. Note that the f(i-2)'s at lower levels are evaluated as part of the next higher level f(i-1). – Richard Mar 06 '15 at 05:23
1

If you follow every recursion to its end, its always at most one path of the fibonacci tree. The stack will develop like this (red edge means a value is stored in memory):

enter image description here enter image description here enter image description here enter image description here enter image description here enter image description here enter image description here

and so on..

For a full binary tree, the length for each path is log_2(X) where X is the number of nodes. Now the total numbers for input n is X=2^n. Now that gives that each path is log_2(2^n)= n long.

Adam
  • 25,960
  • 22
  • 158
  • 247
0

Space complexity of recursive fibonacci algorithm will be the height of the tree which is O(n).

Trick: Only calls that are interlinked with each other will be in the stack at the same time because the previous one will be waiting for the next one to execute and these should be interlinked together at the same time.

Nitin Sharma
  • 1
  • 1