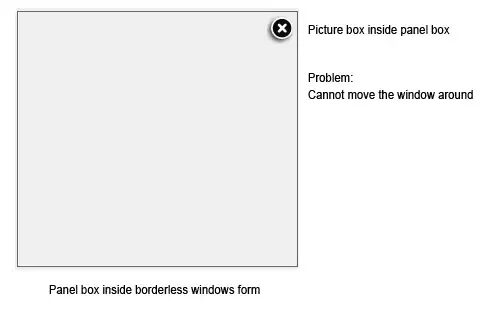
You have two issues:
- A 1-unit displacement between blue and red plots.
- The blue spikes are wider and less tall than the red ones.
How to solve each issue:
This is caused by a possible confusion between the data range 0,...,255 and the indexing interval 1,...,256. Since your data represents an 8-bit image, values should be 0,...,255 (not 1,...,256). Your plotted horizontal axis should then be 0,...,255. Same goes for the i variable in the for line. And then, since Matlab indexing starts at 1, you should use i+1 when indexing pdf_est.
This is normal behaviour. You are assuming unit variance in your kernel. To see taller blue spikes you could reduce sigma to make the kernel narrower and taller. But you will never get the exact same height as your data (the necessary sigma would depend on your data).
Actually, you have a tradeoff between height and width, controlled by sigma. But the important thing is that the area remains the same for any sigma. So I suggest plotting the CDF (area) instead of the pdf (area densisty). To do that, plot the accumulated histogram and pdf (using cumsum).
Code modified according to 1:
function pdf_est=KDE()
close all;
%%Random values of 20 pixels, range=[1 256]
data=randi([1 256],1,20)-1; %// changed: "-1"
%% Estimate histogram%%%%%
pdf_est=zeros(1,256);
z=256;
for i=0:z-1 %// changed_ subtracted 1
for j=1:length(data)
pdf_est(i+1)=pdf_est(i+1)+Gaussian(i-data(j)); %// changed: "+1" (twice)
end
end
%% Plot real histogram 1 to 256; binsize=1;
hold on
plot(0:255, imhist(uint8(data))./length(data),'r'); %// changed: explicit x axis
%% Plot histogram estimation
plot(0:255, pdf_est./length(data),'b'); %// changed: explicit x axis
hold off
function K=Gaussian(x)
sigma=1; %// change? Set as desired
K=1./(sqrt(2*pi)*sigma)*exp(-x^2./(2*sigma^2));
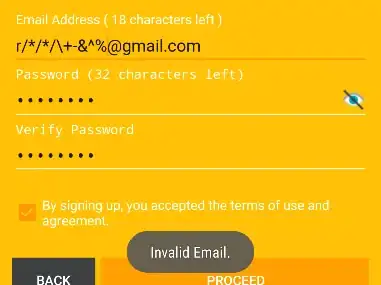
Code modified according to 1 and 2:
function pdf_est=KDE()
close all;
%%Random values of 20 pixels, range=[1 256]
data=randi([1 256],1,20)-1; %// changed: "-1"
%% Estimate histogram%%%%%
pdf_est=zeros(1,256);
z=256;
for i=0:z-1 %// changed: subtracted 1
for j=1:length(data)
pdf_est(i+1)=pdf_est(i+1)+Gaussian(i-data(j)); %// changed: "+1" (twice)
end
end
%% Plot real histogram 1 to 256; binsize=1;
hold on
plot(0:255, cumsum(imhist(uint8(data))./length(data)),'r'); %// changed: explicit x axis
%// changed: cumsum
%% Plot histogram estimation
plot(0:255, cumsum(pdf_est./length(data)),'b'); %// changed: explicit x axis
%// changed: cumsum
hold off
function K=Gaussian(x)
sigma=1; %// change? Set as desired
K=1./(sqrt(2*pi)*sigma)*exp(-x^2./(2*sigma^2));
 where K(.) is Gaussian kernel, data is a given vector. z is bin from 1 to 256. size of bin is 1.
where K(.) is Gaussian kernel, data is a given vector. z is bin from 1 to 256. size of bin is 1.