0

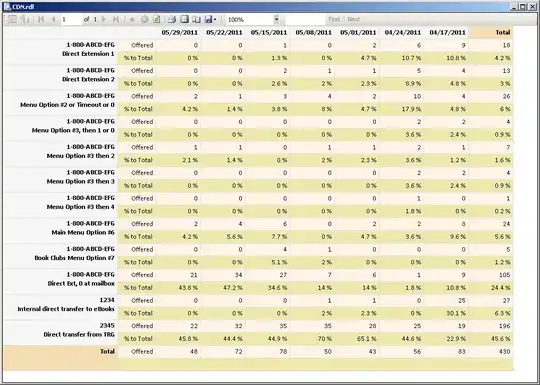
I'm plotting some interaction effects that stem from a regression in stata. I'm using excel for convenience. The data are curvilinear and I'm adding a polynomial trendline to maximize the fit. The problem I have is that the trendline function seems to assume that the x values are 1, 2, 3 and so on. Although in my graph they are actually 0, 0.1, 0.2, and so on. The resulting trendline equation thus does not make much sense.

Example data: X axis: 

0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1

Y axis: 

0.365794061
0.391834869
0.411805232
0.424622483
0.429572487
0.426375536
0.415212526
0.396708002
0.371872294
0.342010179
0.308607579

This gives a trendline (polynomial, 2) of -0.0036x^2 + 0.367x + 0.3336 which neatly fits the data (R^2 is over 99%). However, this equation does not allow me to calculate the maximum correctly.

The data itself stem from a negative binomial regression where the key explanatory variable x is present as linear and quadratic effect (creating the curvilinear shape) with b1 = 0.783 and b2 = -0.953.

So two alternative questions:

1) Is there a way to fix, override, or circumvent the assumption in excel upon which the trendlines are based?

2) Is there a better way of deriving the actual shape of the curve straight from the coefficients of the negative binomial regression?

Thanks,

Simon

SJDS
  • 1,239
  • 1
  • 16
  • 31
  • How did you derive that equation. I get a different one from the graph, using your posted data and adding in an initial x-axis value of zero. `y = -0.3566x^2 + 0.2952x + 0.3667` – Ron Rosenfeld Feb 09 '15 at 07:46
  • I also get different values for the equation using 1, 2 , 3 for the x-values compared with the values you posted, so I don't understand why you conclude that Excel uses integers in place of the actual values. Given your data, I calculate a maximum Y of `0.427791256`. Does that make sense to you? – Ron Rosenfeld Feb 09 '15 at 08:39
  • Hi Ron, thanks for your comment. Your results do make sense to me, which is why I don;t understand that I get completely different ones. I am doing exactly the same (including the initial x-axis value of zero) and I get the equation I posted as an outcome. All I do is select the y column - insert, line, first type - and then add the x axis via select data. Then I select add trendline, polynomial and I get what I get. the 0.427 is indeed what I expect to see, no idea why my results are so different. – SJDS Feb 10 '15 at 02:58
  • Try Inserting a Scatter graph – Ron Rosenfeld Feb 10 '15 at 02:59

1 Answers1

1

Perhaps this will help:

If your version of Excel is 2007 or later, you can use the TREND function which I will demonstrate below.

But to do this graphically, first Insert a Scatter Graph using your x-y coordinates; add a polynomial order 2 trendline, and show the formula. (I also formatted the trendline so it could be visualized, as it is a very close fit:

Scatter Graph with trendline

Then reformat the label as showing digits with 15 decimal places (Excel's precision limit), and copy/paste those values to worksheet cells.

m and b statistics

In A20 enter some new_X value to be used in the formula. Use those statistics in a formula:

Using raw statistics

Or, merely use the TREND function for a polynomial 2nd order, again referencing A20 for a new_X

=TREND(B2:B12,A2:A12^{1,2},A20^{1,2})

Finally, to get the max value of Y, use Solver to maximize either the cell in which the TREND formula is located, or the cell in which you SUM the trendline coefficients

enter image description here

Ron Rosenfeld
  • 53,870
  • 7
  • 28
  • 60
  • Hi, thanks again. It's indeed the scatter graph that makes the difference. When doing that the figure looks exactly the same but the trendline is what you say. Thanks so much. No idea why the line graph doesn't work but the scatterplot seems to do the trick. Thanks a lot,. – SJDS Feb 10 '15 at 03:02
  • To calculate the optimal x-value i simply use the derivative equal to zero, --> m1 / -2m2. :) Problem solved, much appreciated! – SJDS Feb 10 '15 at 03:03
  • @simon_icl With the Line graph, you are only changing the x-axis labels, and not the x-axis values. It is designed for textual labels on the x-axis. Examine Excel HELP for a complete description – Ron Rosenfeld Feb 10 '15 at 03:07
  • @simon_icl As another approach, you can use LINEST to obtain the coefficients. So the optimal x would be `=INDEX(LINEST($B$2:$B$12,$A$2:$A$12^{1,2}),1,2)/(-2*LINEST($B$2:$B$12,$A$2:$A$12^{1,2}))` – Ron Rosenfeld Feb 10 '15 at 03:15
  • Aha, nice one. That's indeed going to be more convenient than always copy pasting the values from the graph! – SJDS Feb 10 '15 at 03:17
  • @simon_icl Just take care to ensure that this is always being done on versions of Excel => 2007. Earlier versions used a less accurate algorithm for LINEST, if I recall correctly. – Ron Rosenfeld Feb 10 '15 at 03:19