I have a list of coordinate to be sorted with a spiral algorithm. My need is to start on the middle of the area and "touch" any coordinate.
To simplify this is the representation of the (unsorted) list of coordinates (x,y marked with a "dot" on following image).
CSV list of coordinates is available here.
X increase from left to right
Y increases from TOP to BOTTOM
 Every coordinate is not adjacent to the following one but are instead distanciated by 1 or 2 dice (or more in certain case).
Every coordinate is not adjacent to the following one but are instead distanciated by 1 or 2 dice (or more in certain case).
Starting from the center of the area, I need to touch any coordinate with a spiral movement:

to parse each coordinate I've drafted this PHP algorithm:
//$missing is an associative array having as key the coordinate "x,y" to be touched
$direction = 'top';
$distance = 1;
$next = '128,127'; //starting coordinate
$sequence = array(
$next;
)
unset($missing[$next]);
reset($missing);
$loopcount = 0;
while ($missing) {
for ($loop = 1; $loop <= 2; $loop++) {
for ($d = 1; $d <= $distance; $d++) {
list($x,$y) = explode(",", $next);
if ($direction == 'top') $next = ($x) . "," . ($y - 1);
elseif ($direction == 'right') $next = ($x + 1) . "," . ($y);
elseif ($direction == 'bottom') $next = ($x) . "," . ($y + 1);
elseif ($direction == 'left') $next = ($x - 1) . "," . ($y);
if ($missing[$next]) {
unset($missing[$next]); //missing is reduced every time that I pass over a coordinate to be touched
$sequence[] = $next;
}
}
if ($direction == 'top') $direction = 'right';
elseif ($direction == 'right') $direction = 'bottom';
elseif ($direction == 'bottom') $direction = 'left';
elseif ($direction == 'left') $direction = 'top';
}
$distance++;
}
but as coordinate are not equidistant from each other, I obtain this output:
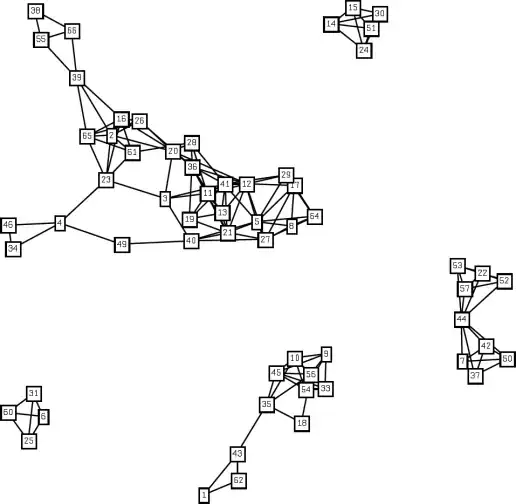
As is clearly visible, the movement in the middle is correct whereas and accordingly with the coordinate position, at a certain instant the jump between each coordinate are not anymore coherent.
How can I modify my code to obtain an approach like this one, instead?
To simplify/reduce the problem: Imagine that dots on shown above image are cities that the salesman have to visit cirurarly. Starting from the "city" in the middle of the area, the next cities to be visited are the ones located near the starting point and located on North, East, Soutch and West of the starting point. The salesman cannot visit any further city unless all the adjacent cities in the round of the starting point hadn't been visited. All the cities must be visited only one time.