How to connect a line between 4 randomly placed points on a plane such that the line does not cross itself

Question

You get 4 coordinates of points on a plain. You need to connect them all with a line. The line must not cross itself.

What's your strategy?

See image

My first intuition was to organize the points as "Top left", "Top right", "Bottom left" and "Bottom right" and continue to connect them so that the top left goes to the bottom left, the bottom left to the bottom right, the bottom right to the top right, and the top right connects back to the top left.

This works in most cases, but not in all. Is there a better strategy?

Thank you all.

Answer 1

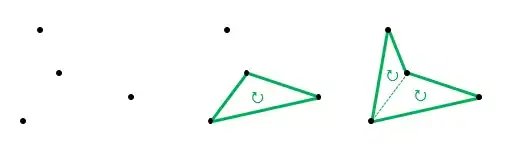
Take three points and form a clockwise triangle (compute the area as the cross product of two sides - if negative, swap two vertexes).

The take the fourth point and compute the areas of the triangles it forms with every (oriented) side of the former. When you find a negative area, insert the new vertex in this side and you are done.

It can turn out that you find no negative area, meaning that the fourth point is inside the triangle. You can insert it in any side.

if Area(P0, P1, P2) < 0
  Swap(P0, P1)

if Area(P0, P1, P3) < 0
  Solution: P0-P3-P1-P2
else if Area(P1, P2, P3) < 0
  Solution: P1-P3-P2-P0
else if Area(P2, P0, P3) < 0
  Solution: P2-P3-P0-P1
else
  Solution: P0-P1-P2-P3

UPDATE

You can think of it using the so-called locus approach. Assume you have formed and oriented a triangle and wish to insert the fourth point. Selecting an edge where you would insert, you can sketch all places where insertion will not cause the sides to cross.

Seeing the shape of the allowed region, you observe that it is the union of the half plane against the insertion side, and the original triangle.

The three lines of support of the triangle partition the plane in 7 regions. Inside any region, you have the choice between 1, 2 or 3 possibilities of insertion in a side (on the figure, we are in a region of type 1).

This apparently contrived approach shows you that you must compare the fourth point against the triangle sides (area test), and in the worst case you can't avoid comparing against the three of them.

The shape of the boundaries tell you what kind of equations you will need to use, and the number of regions hints you how many tests you will have to perform.

Answer 2

Well, I haven't gamed it out enough to be 100% sure, but I think the following would work:

• Choose a point.
• Subtract it from each other point to get the 3 vectors to the 3 other points.
• Use dot products and magnitudes to determine the angle between each pair of vectors (3 pairs for the 3 dots).
• Connect the point to the 2 other points with the greatest angle between their vectors.
• Connect the remaining point to those 2 points also.

So far, I haven't come up with an example where that fails, but maybe that's just because it's too late at night for me. :)

Quick note:

A dot B = ax*bx + ay*by [ + az*bz ... ] = |A||B|cos(angle_between_A_and_B)

To make calculation more efficient:

First, since the dot product only gives you angles from 0 to 180 degrees, you can check which angle is larger by checking which cosine is smaller, or more negative. This avoids needing to perform an arc cosine.

That still requires you to perform a sqrt function for each magnitude, since the dot product gives you |A||B|cos(angle), and you have to divide by |A||B| to get the cosine. However, with a little heuristics, we can avoid the sqrt as well. |A| and |B| must always be positive. So:

• If one dot product is negative and the other is positive, then the negative dot product must have a negative cosine, and the other have a positive cosine, so the negative one is a larger angle.

• If they are both positive, then you can square the dot products, and then divide by the magnitudes squared (x^2 + y^2 [+ z^2...] without the sqrt). The smaller result will be the smaller cosine, and so the larger angle.

• If the dot products are both negative, you perform the same operation, but then the larger result will be the smaller cosine, and so the larger angle.