Here's my code:
#data
sites <-
structure(list(site = c(928L, 928L, 928L, 928L, 928L, 928L, 928L,
928L, 928L, 928L, 928L, 928L, 928L, 928L,
928L, 928L, 928L, 928L, 928L, 928L, 928L,
928L, 928L, 928L, 928L, 928L),
date = c(13493L, 13534L, 13566L, 13611L, 13723L,
13752L, 13804L, 13837L, 13927L, 14028L,
14082L, 14122L, 14150L, 14182L, 14199L,
16198L, 16279L, 16607L, 16945L, 17545L,
17650L, 17743L, 17868L, 17941L, 18017L, 18092L),
y = c(7L, 7L, 17L, 18L, 17L, 17L, 10L, 3L, 17L, 24L,
11L, 5L, 5L, 3L, 5L, 14L, 2L, 9L, 9L, 4L, 7L,
6L, 1L, 0L, 5L, 0L)),
.Names = c("site", "date", "y"),
class = "data.frame", row.names = c(NA, -26L))
#convert to date
x<-as.Date(sites$date, origin="1960-01-01")
#plot smooth, line goes below zero!
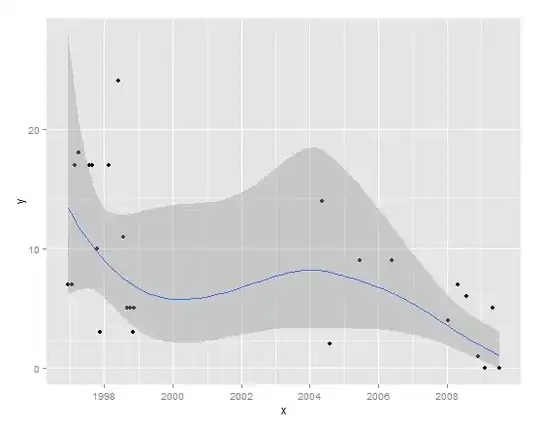
qplot(data=sites, x, y, main="Site 349")
(p <- qplot(data = sites, x, y, xlab = "", ylab = ""))
(p1 <- p + geom_smooth(method = "loess",span=0.5, size = 1.5))
Some of the LOESS lines and confidence intervals go below zero, I would like to restrict the graphics to 0 and positive numbers (because negative do not make sense).
How can I do this?