How to sum sequence?

Question

How can I sum the following sequence:

⌊n/1⌋ + ⌊n/2⌋ + ⌊n/3⌋ + ... + ⌊n/n⌋

This is simply O(n) solution on C++:

#include <iostream>
int main()
{
   int n;
   std::cin>>n;
   unsigned long long res=0;
   for (int i=1;i<=n;i++)
   {
      res+= n/i;
   }
   std::cout<<res<<std::endl;
   return 0;
}

Do you know any better solution than this? I mean O(1) or O(log(n)). Thank you for your time :) and solutions

Edit: Thank you for all your answers. If someone wants the solution O(sqrt(n)): Python:

import math
def seq_sum(n):
 sqrtn = int(math.sqrt(n))
 return sum(n // k for k in range(1, sqrtn + 1)) * 2 - sqrtn ** 2
n = int(input())
print(seq_sum(n))

C++:

#include <iostream>
#include <cmath>
int main()
{
   int n;
   std::cin>>n;
   int sqrtn = (int)(std::sqrt(n));
   long long res2 = 0;
   for (int i=1;i<=sqrtn;i++)
   {
      res2 +=2*(n/i);
   }
   res2 -= sqrtn*sqrtn;
   std::cout<<res2<<std::endl;
   return 0;
}

Answer 1

This is Dirichlet's divisor summatory function D(x). Using the following formula (source)

where

gives the following O(sqrt(n)) psuedo-code (that happens to be valid Python):

def seq_sum(n):
  sqrtn = int(math.sqrt(n))
  return sum(n // k for k in range(1, sqrtn + 1)) * 2 - sqrtn ** 2

Notes:

• The // operator in Python is integer, that is truncating, division.
• math.sqrt() is used as an illustration. Strictly speaking, this should use an exact integer square root algorithm instead of floating-point maths.

Answer 2

Taken from the Wikipedia article on the Divisor summatory function,

where . That should provide an time solution.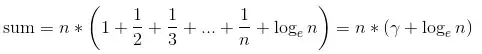

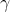EDIT: the integer square root problem can also be solved in square root or even logarithmic time too - just in case that isn't obvious.

Answer 3

The Polymath project sketches an algorithm for computing this function in time O(n^(1/3 + o(1))), see section 2.1 on pages 8-9 of:

http://arxiv.org/abs/1009.3956

The algorithm involves slicing the region into sufficiently thin intervals and estimating the value on each, where the intervals are chosen to be thin enough that the estimate will be exact when rounded to the nearest integer. So you compute up to some range directly (they suggest 100n^(1/3) but you could modify this with some care) and then do the rest in these thin slices.

See the OEIS entry for more information on this sequence.

Edit: I now see that Kerrek SB mentions this algorithm in the comments. In fairness, though, I added the comment to the OEIS 5 years ago so I don't feel bad for posting 'his' answer. :)

I should also mention that no O(1) algorithm is possible, since the answer is around n log n and hence even writing it out takes time > log n.

Answer 4

Let's divide all number {1, 2, 3, ..., n} into 2 groups: less than or equal to sqrt(n) and greater than sqrt(n). For the first group, we can compute the sum by simple iteration. For the second group, we can use the following observation: if a > sqrt(n), than n / a < sqrt(n). That's why we can iterate over the value of [n / i] = d (from 1 to sqrt(n)) and compute the number of such i that [n / i] = d. It can be found in O(1) for a fixed d using the fact that [n / i] = d means i * d <= n and i * (d + 1) > n, which gives [n / (d + 1)] < i <= [n / d].

The first and the second groups are processed in O(sqrt(n)), which gives O(sqrt(n)) time in total.

Answer 5

For large n, use the formula:

where

( is a transcendental number.)

See the Euler-Mascheroni constant article for more information.

Answer 6

You can notice that there is O(n^(1/2)) unique values in the set S = {⌊n/1⌋, ⌊n/2⌋, ..., ⌊n/(n-1)⌋, ⌊n/n⌋}. Therefore you can calculate the function in O(n^(1/2))

Also since this function is asymmetric, you can even calculate x2 faster by using this formula: D(n) = Σ(x=1->u)(⌊n/x⌋) - u^2 for u = ⌊n^(1/2)⌋

Even more complex but faster: using the method that Richard Sladkey described in this paper you can calculate the function in O(n^(1/3))