How to speed up calculation of length of longest common substring?

Question

I have two very large strings and I am trying to find out their Longest Common Substring.

One way is using suffix trees (supposed to have a very good complexity, though a complex implementation), and the another is the dynamic programming method (both are mentioned on the Wikipedia page linked above).

Using dynamic programming

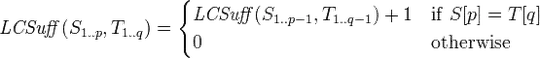
The problem is that the dynamic programming method has a huge running time (complexity is O(n*m), where n and m are lengths of the two strings).

What I want to know (before jumping to implement suffix trees): Is it possible to speed up the algorithm if I only want to know the length of the common substring (and not the common substring itself)?

Answer 1

These will make it run faster, though it'll still be O(nm).

One optimization is in space (which might save you a little allocation time) is noticing that LCSuff only depends on the previous row -- therefore if you only care about the length, you can optimize the O(nm) space down to O(min(n,m)).

The idea is to keep only two rows -- the current row that you are processing, and the previous row that you just processed, and throw away the rest.

Answer 2

Will it be faster in practice? Yes. Will it be faster regarding Big-Oh? No. The dynamic programming solution is always O(n*m).

The problem that you might run into with suffix trees is that you trade the suffix tree's linear time scan for a huge penalty in space. Suffix trees are generally much larger than the table you'd need to implement for a dynamic programming version of the algorithm. Depending on the length of your strings, it's entirely possible that dynamic programming will be faster.

Good luck :)

Answer 3

Here's a simple algorithm which can finishes in O((m+n)*log(m+n)), and much easier to implement compared to suffix tree algorithm which is O(m+n) runtime.

let it start with min common length (minL) = 0, and max common length (maxL) = min(m+n)+1.

1. if (minL == maxL - 1), the algorithm finished with common len = minL.

2. let L = (minL + maxL)/2

3. hash every substring of length L in S, with key = hash, val = startIndex.

4. hash every substring of length L in T, with key = hash, val = startIndex. check if any hash collision in to hashes. if yes. check whether whether they are really common substring. 

5. if there're really common substring of length L, set minL = L, otherwise set maxL = L. goto 1.

The remaining problem is how to hash all substring with length L in time O(n). You can use a polynomial formula as follow:

Hash(string s, offset i, length L) = s[i] * p^(L-1) + s[i+1] * p^(L-2) + ... + s[i+L-2] * p + s[i+L-1]; choose any constant prime number p.

then Hash(s, i+1, L) = Hash(s, i, L) * p - s[i] * p^L + s[i+L];

Answer 4

Myer's bit vector algorithm can help you. It works by using bit manipulation and is a much faster approach.