Back-propagation does not use the error values directly. What you back-propagate is the partial derivative of the error with respect to each element of the neural network. Eventually that gives you dE/dW for each weight, and you make a small step in the direction of that gradient.
To do this, you need to know:
The activation value of each neuron (kept from when doing the feed-forward calculation)
The mathematical form of the error function (e.g. it may be a sum of squares difference). Your first set of derivatives will be dE/da for the output layer (where E is your error and a is the output of the neuron).
The mathematical form of the neuron activation or transfer function. This is where you discover why we use sigmoid because dy/dx of the sigmoid function can conveniently be expressed in terms of the activation value, dy/dx = y * (1 - y) - this is fast and also means you don't have to store or re-calculate the weighted sum.
Please note, I am going to use different notation from you, because your labels make it hard to express the general form of back-propagation.
In my notation:
Superscripts in brackets (k) or (k+1) identify a layer in the network.
There are N neurons in layer (k), indexed with subscript i
There are M neurons in layer (k+1), indexed with subscript j
The sum of inputs to a neuron is z
The output of a neuron is a
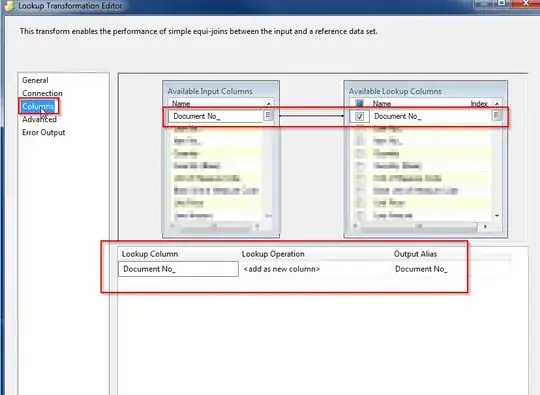
A weight is Wij and connects ai in layer (k) to zj in layer (k+1). Note W0j is the weight for bias term, and sometimes you need to include that, although your diagram does not show bias inputs or weights.
With the above notation, the general form of the back-propagation algorithm is a five-step process:
1) Calculate initial dE/da for each neuron in the output layer. Where E is your error value, and a is the activation of the neuron. This depends entirely on your error function.
Then, for each layer (start with k = maximum, your output layer)
2) Backpropagate dE/da to dE/dz for each neuron (where a is your neuron output and z is the sum of all inputs to it including the bias) within a layer. In addition to needing to know the value from (1) above, this uses the derivative of your transfer function:
(Now reduce k by 1 for consistency with the remainder of the loop):
3) Backpropagate dE/dz from an upper layer to dE/da for all outputs in previous layer. This basically involves summing across all weights connecting that output neuron to the inputs in the upper layer. You don't need to do this for the input layer. Note how it uses the value you calculated in (2)
4) (Independently of (3)) Backpropagate dE/dz from an upper layer to dE/dW for all weights connecting that layer to the previous layer (this includes the bias term):
Simply repeat 2 to 4 until you have dE/dW for all your weights. For more advanced networks (e.g. recurrent), you can add in other error sources by re-doing step 1.
5) Now you have the weight derivatives, you can simply subtract them (times a learning rate) to take a step towards what you hope is the error function minimum:
The maths notation can seem a bit dense in places the first time you see this. But if you look a few times, you will see there are essentially only a few variables, and they are indexed by some combination of i, j, k values. In addition, with Matlab, you can express vectors and matrices really easily. So for instance this is what the whole process might look like for learning a single training example:
clear ; close all; clc; more off
InputVector = [ 0.5, 0.2 ];
TrainingOutputVector = [ 0.1, 0.9 ];
learn_rate = 1.0;
W_InputToHidden = randn( 3, 2 ) * 0.6;
W_HiddenToOutput = randn( 3, 2 ) * 0.6;
for i=1:20,
% Feed-forward input to hidden layer
InputsPlusBias = [1, InputVector];
HiddenActivations = 1.0 ./ (1.0 + exp(-InputsPlusBias * W_InputToHidden));
% Feed-forward hidden layer to output layer
HiddenPlusBias = [ 1, HiddenActivations ];
OutputActivations = 1.0 ./ (1.0 + exp(-HiddenPlusBias * W_HiddenToOutput));
% Backprop step 1: dE/da for output layer (assumes mean square error)
OutputActivationDeltas = OutputActivations - TrainingOutputVector;
nn_error = sum( OutputActivationDeltas .* OutputActivationDeltas ) / 2;
fprintf( 'Epoch %d, error %f\n', i, nn_error);
% Steps 2 & 3 combined:
% Back propagate dE/da on output layer to dE/da on hidden layer
% (uses sigmoid derivative)
HiddenActivationDeltas = ( OutputActivationDeltas * W_HiddenToOutput(2:end,:)'
.* ( HiddenActivations .* (1 - HiddenActivations) ) );
% Steps 2 & 4 combined (twice):
% Back propagate dE/da to dE/dW
W_InputToHidden_Deltas = InputsPlusBias' * HiddenActivationDeltas;
W_HiddenToOutput_Deltas = HiddenPlusBias' * OutputActivationDeltas;
% Step 5: Alter the weights
W_InputToHidden -= learn_rate * W_InputToHidden_Deltas;
W_HiddenToOutput -= learn_rate * W_HiddenToOutput_Deltas;
end;
As written this is stochastic gradient descent (weights altering once per training example), and obviously is only learning one training example.
Apologies for pseudo-math notation in places. Stack Overflow doesn't have simple built in LaTex-like maths, unlike Math Overflow. I have skipped some of the derivation/explanation for steps 3 and 4 to avoid this answer taking forever.