Calculating the angle between a line and the x-axis

Question

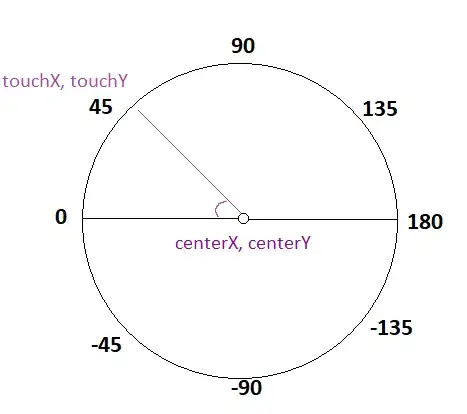
I'm currently developing a simple 2D game for Android. I have a stationary object that's situated in the center of the screen and I'm trying to get that object to rotate and point to the area on the screen that the user touches. I have the constant coordinates that represent the center of the screen and I can get the coordinates of the point that the user taps on. I'm using the formula outlined in this forum: How to get angle between two points?

• It says as follows "If you want the the angle between the line defined by these two points and the horizontal axis:

  double angle = atan2(y2 - y1, x2 - x1) * 180 / PI;".
  

• I implemented this, but I think the fact the I'm working in screen coordinates is causing a miscalculation, since the Y-coordinate is reversed. I'm not sure if this is the right way to go about it, any other thoughts or suggestions are appreciated.

Answer 1

Assumptions: x is the horizontal axis, and increases when moving from left to right. y is the vertical axis, and increases from bottom to top. (touch_x, touch_y) is the point selected by the user. (center_x, center_y) is the point at the center of the screen. theta is measured counter-clockwise from the +x axis. Then:

delta_x = touch_x - center_x
delta_y = touch_y - center_y
theta_radians = atan2(delta_y, delta_x)

Edit: you mentioned in a comment that y increases from top to bottom. In that case,

delta_y = center_y - touch_y

But it would be more correct to describe this as expressing (touch_x, touch_y) in polar coordinates relative to (center_x, center_y). As ChrisF mentioned, the idea of taking an "angle between two points" is not well defined.

Answer 2

Had a need for similar functionality myself, so after much hair pulling I came up with the function below

/**
 * Fetches angle relative to screen centre point
 * where 3 O'Clock is 0 and 12 O'Clock is 270 degrees
 * 
 * @param screenPoint
 * @return angle in degress from 0-360.
 */
public double getAngle(Point screenPoint) {
    double dx = screenPoint.getX() - mCentreX;
    // Minus to correct for coord re-mapping
    double dy = -(screenPoint.getY() - mCentreY);

    double inRads = Math.atan2(dy, dx);

    // We need to map to coord system when 0 degree is at 3 O'clock, 270 at 12 O'clock
    if (inRads < 0)
        inRads = Math.abs(inRads);
    else
        inRads = 2 * Math.PI - inRads;

    return Math.toDegrees(inRads);
}

Answer 3

A few answers here have tried to explain the "screen" issue where top left is 0,0 and bottom right is (positive) screen width, screen height. Most grids have the Y axis as positive above X not below.

The following method will work with screen values instead of "grid" values. The only difference to the excepted answer is the Y values are inverted.

/**
 * Work out the angle from the x horizontal winding anti-clockwise 
 * in screen space. 
 * 
 * The value returned from the following should be 315. 
 * <pre>
 * x,y -------------
 *     |  1,1
 *     |    \
 *     |     \
 *     |     2,2
 * </pre>
 * @param p1
 * @param p2
 * @return - a double from 0 to 360
 */
public static double angleOf(PointF p1, PointF p2) {
    // NOTE: Remember that most math has the Y axis as positive above the X.
    // However, for screens we have Y as positive below. For this reason, 
    // the Y values are inverted to get the expected results.
    final double deltaY = (p1.y - p2.y);
    final double deltaX = (p2.x - p1.x);
    final double result = Math.toDegrees(Math.atan2(deltaY, deltaX)); 
    return (result < 0) ? (360d + result) : result;
}

Answer 4

in android i did this using kotlin:

private fun angleBetweenPoints(a: PointF, b: PointF): Double {
        val deltaY = abs(b.y - a.y)
        val deltaX = abs(b.x - a.x)
        return Math.toDegrees(atan2(deltaY.toDouble(), deltaX.toDouble()))
    }

Answer 5

fun calculateAngle(
    touchX: Float,
    touchY: Float,
    centerX: Float,
    centerY: Float
): Float {
    val deltaX = centerX - touchX
    val deltaY = centerY - touchY
    return Math.toDegrees(atan2(deltaY.toDouble(), deltaX.toDouble())).toFloat()
}

This function will return value like

If we + 180 to the return value then we will get the value from right to left like

360(<=> 0) -> 45 -> 90 -> 135 -> 180 -> 225 -> 270 -> 315

similar to the angle when we drawArc

Answer 6

"the origin is at the top-left of the screen and the Y-Coordinate increases going down, while the X-Coordinate increases to the right like normal. I guess my question becomes, do I have to convert the screen coordinates to Cartesian coordinates before applying the above formula?"

If you were calculating the angle using Cartesian coordinates, and both points were in quadrant 1 (where x>0 and y>0), the situation would be identical to screen pixel coordinates (except for the upside-down-Y thing. If you negate Y to get it right-side up, it becomes quadrant 4...). Converting screen pixel coordinates to Cartesian doesnt really change the angle.

Answer 7

with pygame:

dy = p1.y - p2.y
dX = p2.x - p1.x

rads = atan2(dy,dx)
degs = degrees(rads)
if degs < 0 :
   degs +=90

it work for me

Answer 8

If you wanto get slope as radian -> m = math.atan2((jy-iy),(jx-ix))

and degree ---> m = math.atan2((jy-iy),(jx-ix))*180/math.pi