I'm working on a problem (from Introduction to Automata Theory, Languages and Computer by Hopcroft, Motwani and Ullman) to write a regular expression that defines a language consisting of all strings of 0s and 1s not containing the substring 011.
Is the answer (0+1)* - 011 correct ? If not what should be the correct answer for this?
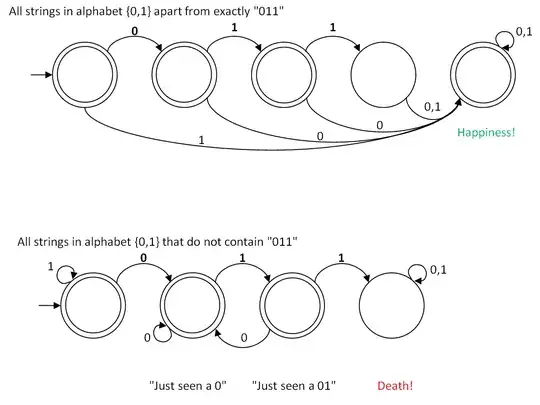 Edit: Updated to include start states and fixes, as per below comments.
Edit: Updated to include start states and fixes, as per below comments.