CGAL triangulation fails

Question

I am starting to use CGAL to triangulate a set of points using the following code

#include <iostream>
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Delaunay_triangulation_2.h>
#include <CGAL/Triangulation_vertex_base_with_info_2.h>

typedef CGAL::Exact_predicates_inexact_constructions_kernel K;
typedef CGAL::Triangulation_vertex_base_2<K> Vb;
typedef CGAL::Triangulation_face_base_2<K> Fb;
typedef CGAL::Triangulation_data_structure_2<Vb,Fb> Tds;
typedef CGAL::Delaunay_triangulation_2<K,Tds> Triangulation;

typedef Triangulation::Point Point;
typedef Triangulation::Triangulation_data_structure tds;


using namespace std;


void main()
{
    Triangulation t;
    t.insert(Point(0,0));
    t.insert(Point(0,20));
    t.insert(Point(30,15));
    t.insert(Point(30,-15));

    Triangulation::Finite_faces_iterator fib = t.finite_faces_begin(), it;
    Triangulation::Finite_faces_iterator fie = t.finite_faces_end();
    Triangulation::Triangle tri;
    std::cout << "Triangular faces"<<endl;
    for (it=fib; it!=fie; ++it)
    {
        tri = t.triangle(it);
        std::cout<<tri[0]<<" "<<tri[1]<<" "<<tri[2]<<" "<<endl;
    }   
    char c;
    std::cin>>c;
}

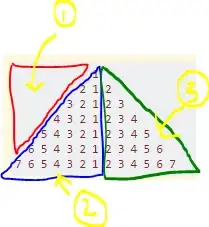
This prints the faces as 0,20 0,0 30,15 and 0,0 30,-15 30,15. I am not satisfied with this output as the first triangle is completely inside the second. As I understand triangulation it should return 3 triangles and not just 2 covering the complex hull of my 4 input points, and there should be no overlapping triangles. Could someone explain what I am doing wrong ?

My ultimate goal is to triangulate a convex polygon under a minimum angle constraint (and by addin additional points to the set). Any CGAL code sample would be appreciated.

Thanks,

Answer 1

I don't think you quite understand the geometry going on here, or triangulation, so I've drawn up some pictures.

Here's your setup:

Here's the first triangle that the Delaunay_Triangulation_2 generated:

(0,20), (0,0), (30, 15)

And here's the second triangle generated:

(0,0) (30,-15) (30,15)

Clearly, neither triangle is contained within the other. Also, the union of the triangles, removing the shared edge, perfectly creates the convex hull of the points.

Also, given that you only have four points total, it is impossible to construct a triangulation of 3 triangles where none overlap, hence only 2 are created.