Explanation of Self-healing property of CBC (Cipher Block Chaining)

Question

Wikipedia:

CBC mode has the self-healing property: if one block of the cipher is altered, the error propagates for at most two blocks.

Made up Example:

Let the block size be 64 bits. The original plaintext is:

3231343336353837  3231343336353837  3231343336353837  • • •

The correct cipher text is:

ef7c4bb2b4ce6f3b  f6266e3a97af0e2c  746ab9a6308f4256 • • •

If the ciphertext is corrupted, with the byte '0x4b' changed to '0x4c':

ef7c4cb2b4ce6f3b  f6266e3a97af0e2c  746ab9a6308f4256  • • •

Then it is decrypted to:

efca61e19f4836f1  3231333336353837  3231343336353837  • • •

Question:

I am having hard time understanding the self-healing property of CBC (Cipher Block Chaining), I thought that a made up example might help but I am now more confused. Any help would be great.

Your question would be even better, if you would provide the code to generate your example, including the IV and key, so others would know how to reproduce your example. I assume you have used DES? — Perseids, Oct 11 '14 at 22:34

Perseids · Accepted Answer · 2014-10-11T22:47:19.313

Personally, I find the decryption graphics very helpful for such kind of questions. From the Wikipedia (public domain image):

Original CBC decryption

Now let's add some corruption:

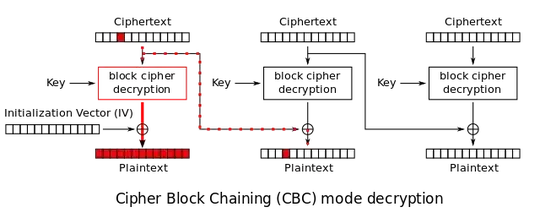
Corrupted CBC decryption

The red dots represent partial corrupted inputs, while the solid red line represents complete block corruption.

Some notation before we start: I'll number the original plaintext blocks as p1 through p3, the corrupted ones as p1' through p3', the correct ciphertext blocks as c1 through c3 and the corrupted ones as c1' through c3':

3231343336353837  3231343336353837  3231343336353837  • • •
       p1                p2                 p3

ef7c4bb2b4ce6f3b  f6266e3a97af0e2c  746ab9a6308f4256  • • •
       c1                c2                 c3

ef7c4cb2b4ce6f3b  f6266e3a97af0e2c  746ab9a6308f4256  • • •
       c1'               c2'=c3             c3'=c3

efca61e19f4836f1  3231333336353837  3231343336353837  • • •
       p1'               p2'                p3'=p3

There is also some IV that you have not given in your example.

Let's take a look at the first block: Three bits in the input of the block cipher are changed (0x4b ^ 0x4c = 0x07 = 4+2+1). As a block cipher is designed to be a pseudo random permutation - that is a bijective function being indistinguishable from a random function (without knowledge of the key k) - we get a completely (pseudo) random block as output of the decryption function:

    dec(      c1        ,k) =         p1       XOR IV
<=> dec(ef7c4bb2b4ce6f3b,k) = 3231343336353837 XOR IV
    dec(      c1'       ,k) =         p1'      XOR IV
<=> dec(ef7c4cb2b4ce6f3b,k) = efca61e19f4836f1 XOR IV

As a next step the IV is XORed, so we end up with

    dec(      c1        ,k) XOR IV =         p1       
<=> dec(ef7c4bb2b4ce6f3b,k) XOR IV = 3231343336353837 
    dec(      c1'       ,k) XOR IV =         p1'      
<=> dec(ef7c4cb2b4ce6f3b,k) XOR IV = efca61e19f4836f1

which shows that the whole block was destroyed (complete red block at the bottom).

Now, on to the second block: We start again by decrypting the ciphertext block, which works fine as no corruption has occurred in the block:

    dec(      c2        ,k) =         p2       XOR         c1
<=> dec(f6266e3a97af0e2c,k) = 3231343336353837 XOR ef7c4bb2b4ce6f3b
                                                    ^

Notice that this formula uses non-corrupted blocks everywhere. As a reminder, this block was generated like this during encryption:

             c2      = enc(        p2       XOR         c1      ,k)
<=> f6266e3a97af0e2c = enc(3231343336353837 XOR ef7c4bb2b4ce6f3b,k)

The next step is again the application of the XOR with the previous block (this time not the IV, but c1'). This previous block c1' is corrupted:

    dec(      c2        ,k) XOR       c1'        =         p2       XOR         c1       XOR        c1'
<=> dec(f6266e3a97af0e2c,k) XOR ef7c4cb2b4ce6f3b = 3231343336353837 XOR ef7c4bb2b4ce6f3b XOR ef7c4cb2b4ce6f3b

Now we can actually calculate c1 XOR c1' (the error) as c1 XOR c1' = 0000007000000000 and replace that everywhere:

    dec(      c2        ,k) XOR       c1'        =         p2       XOR 0000007000000000
<=> dec(f6266e3a97af0e2c,k) XOR ef7c4cb2b4ce6f3b = 3231343336353837 XOR 0000007000000000

And at last simplify p2 XOR 0000007000000000 = p2':

    dec(      c2        ,k) XOR       c1'        =         p2'      
<=> dec(f6266e3a97af0e2c,k) XOR ef7c4cb2b4ce6f3b = 3231333336353837

You see that the original corruption (0x07) to the first ciphertext block c1' is transferred verbatim to the the second plaintext block p2', but it remains otherwise intact (as is visualized by a mostly white block in the graphic, with a single square being red). This peculiar property of CBC can lead to attacks against real world systems, like padding oracle attacks.

The third block is boring as hell: No inputs to the decryption and XOR have changed, thus p1=p1' and everything is fine there.

score 1 · Answer 2 · answered Oct 11 '14 at 21:35

When decrypting in CBC mode a block is decrypted by first deciphering the block in question using the key, and then XOR it with the previous block in the ciphertext. Take a look at the CBC mode drawing on wiki

As you only need the current and previous block for decryptin in CBC mode, the effect of a changed byte in the ciphertext, would only affect the block it's in, and the following block (if that exists).

Explanation of Self-healing property of CBC (Cipher Block Chaining)

2 Answers2