Unexpected error in Julia set rendering

Question

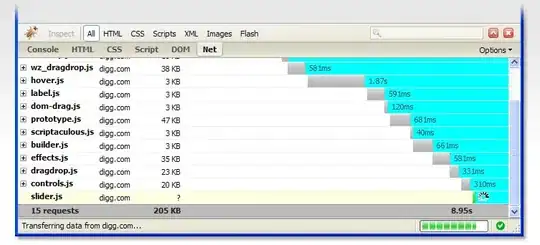
I am playing with Mandelbrot and Julia sets and I encountered interesting problem. The Mandelbrot set can be rendered in double precision until zooms of around 2^56 at any place. However, the Julia set sometimes produces artifacts much sooner like around zoom of 2^20 (see image below).

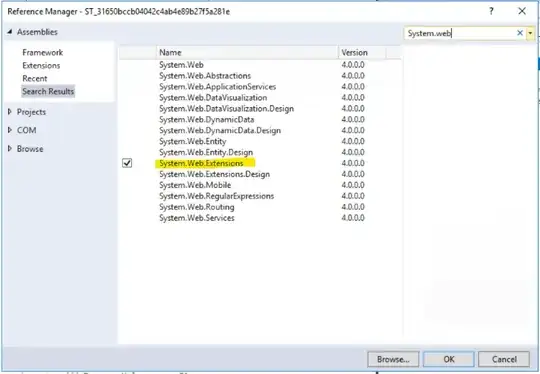
The interesting thing is that this occurs only in some areas but the rest of the image is OK and you can even continue zooming in. This usually happens in the center of clusters and near origin [0,0].

1. Is this really caused by double arithmetic errors?
2. Can one avoid those artifacts without need of use arbitrary precision arithmetic?
3. Why it occurs only in some areas? Are those areas somewhat special?

Coords

I do not have coords of the image above but another one can be found here (pictured below):

• Center = [0, 0]
• Zoom 2^26
• C = [-8.01030596311150589e-01, 1.56495138793530941e-01]

Arbitrary precision

Running the code with arbitrary precision seem to help but only a little. 82 bits of arbitrary precision is better than just double but then 232 bits is exactly the same as 82. Maybe my implementation has flaws? The only number that has lower precision is the argument C that is taken from the Mandelbrot set and it has the precision required to capture it in the depth where it was set - I don't think that this matters because adding extra zeros to make the precision high won't change the result. The immediate variables that are computing the result are all high precision.

Double precision:

Arbitrary precision 82 bits:

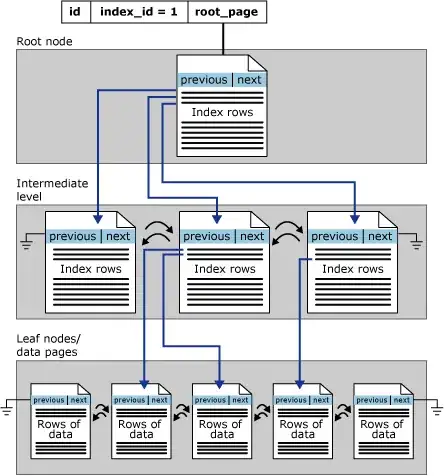
Arbitrary precision 232 bits:

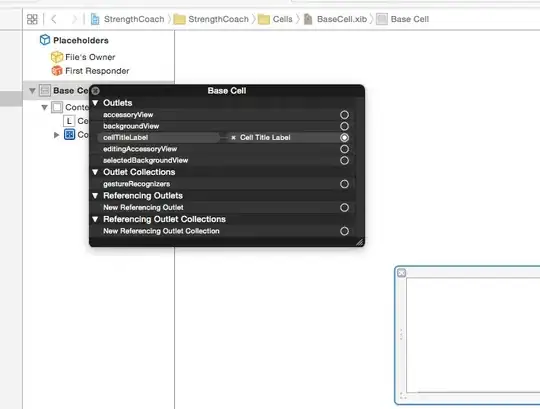
Code

This is the core of my code (unnecessary parts pieces omitted):

public void UberCompute(UberComplex origin, UberComplex size,
        UberComplex initialCoord, int maxIters, double[,] result,
        ref bool stop) {

    int wid = result.GetLength(1);
    int hei = result.GetLength(0);
    int area = wid * hei;

    int precision = Math.Max(origin.Precision,
        initialCoord == null ? 0 : initialCoord.Precision);
    UberComplex coord = new UberComplex(precision);
    UberComplex step = new UberComplex(precision);
    UberFloat.Div(step.Re, size.Re, wid);
    UberFloat.Div(step.Im, size.Im, hei);

    UberFloat imed1 = new UberFloat(precision);
    UberFloat imed2 = new UberFloat(precision);
    UberFloat imed3 = new UberFloat(precision);

    for (int y = 0; y < hei; ++y) {
        // double yt = (double)y / hei;
        // double im = origin.Im + yt * size.Im;
        UberFloat.Mul(imed1, step.Im, y);
        UberFloat.Add(coord.Im, imed1, origin.Im);

        if (stop) {
            break;
        }

        for (int x = 0; x < wid; ++x) {
            // double xt = (double)x / wid;
            // Complex coord = new Complex(origin.Re + xt * size.Re, im);
            UberFloat.Mul(imed1, step.Re, x);
            UberFloat.Add(coord.Re, imed1, origin.Re);

            result[y, x] = UberIterate(initialCoord ?? coord,
                coord, maxIters, smooth, imed1, imed2, imed3);
        }
    }
}

public double UberIterate(UberComplex coord, UberComplex initialCoord, int maxIters,
        UberFloat imed1, UberFloat imed2, UberFloat imed3) {

    Contract.Requires(imed1.Precision == initialCoord.Precision);
    Contract.Requires(imed2.Precision == initialCoord.Precision);
    Contract.Requires(imed3.Precision == initialCoord.Precision);

    int precision = coord.Precision;
    UberFloat re = new UberFloat(precision, initialCoord.Re);
    UberFloat im = new UberFloat(precision, initialCoord.Im);

    int i = 0;
    do {
        // re * re + im * im > maxRadiusSq
        UberFloat.Mul(imed1, re, re);
        UberFloat.Mul(imed2, im, im);
        UberFloat.Add(imed3, imed1, imed2);
        if (imed3 > MAX_RADIUS_SQ) {
            break;
        }

        // newRe = re * re - im * im + coord.Re;
        UberFloat.Sub(imed3, imed1, imed2);
        UberFloat.Add(imed1, imed3, coord.Re);

        // im = 2.0 * re * im + coord.Im;
        UberFloat.Mul(imed2, re, im);
        UberFloat.Mul(imed3, imed2, 2);
        UberFloat.Add(im, imed3, coord.Im);

        // re = newRe;
        UberFloat.Swap(re, imed1);
    } while (++i < maxIters);

    if (i == maxIters) {
        return Double.NaN;  // Did not diverged.
    }

    return i;
}

Other software

I have tested Ultra Fractal and it has this issue as well:

Answer 1

Some time ago I got into rendering several fractals like the Julia set and now I discovered the same phenomenon. Since your question is quite old, I am not sure if this is still interesting to You, but I'll try to explain it.

You already assumed it has to do with limitations of floating poit representation, which is correct. Floating poit representation implies a trade-off between range and precision, as explained in Wikipedia. You can see that the the bigger in magnitude the representable numbers are, the further apart from each other they become. (I can't go in to much detail because I'm not a maths person.)

It is therefore possible to have three different numbers a, b and c that are representable as float where

• a and b are small in magnitude and very close to each other and
• c is much larger such that calculating a + c with floating point arithmetics has the same result as b + c.

This is exactly what happens especially when iterating the function for this Julia set around the origin. To proove that, I took two coordinates p and q from your first image (it seems to be mirrored around the x-axis) and used them as initial values for the algorithm:

p and q choosen from your first image

• p := (-1.5615161e-8, -9.176949e-9)
• q := (-1.3292692e-8, -1.0307186e-8)
• c from your example := (-8.01030596311150589e-01, 1.56495138793530941e-01)

Right at the first iteration I got this (using double precision):

p² = (1.5961686010731998e-16, 2.86599072247578e-16)
p² + c = (-0.8010305963111505, 0.15649513879353122)

q² = (7.045757736826799e-17, 2.7402049776942403e-16)
q² + c = (-0.8010305963111505, 0.15649513879353122)

And there you have it. At the first iteration the numbers become the same. Note that squaring numbers like 10^(-8) leads to even smaller numbers like 10^(-16) which makes the error even more prominent.

I also found other initial values that are further away from the origin and also make the algorithm behave identically after some iterations and wrote a little haskell programm to do the calculation:

import System.Environment
import Data.Complex
import Control.Monad
import Text.Read

main = do
    args <- getArgs
    case processArgs args of
        Just (c, z, r) -> do
            putStrLn $ "c = " ++ show c
            putStrLn $ "z = " ++ show z
            putStrLn $ "escape radius = " ++ show r
            printIteration `mapM_` juliaSequence c z r
        Nothing -> putStrLn "Invalid argument format"

processArgs :: [String] -> Maybe (Complex Double, Complex Double, Double)
processArgs args = do
    when (length args /= 5) Nothing
    [cRe, cIm, zRe, zIm, r] <- readMaybe `mapM` args
    return (cRe :+ cIm, zRe :+ zIm, r)

juliaSequence c z r = (takeWhile inEscapeRadius . tail . iterate julia) (-1, 0, 0, z) where
    julia (nMinus1, _, _, z) = (nMinus1 + 1, z, z2, z2 + c) where z2 = z * z
    inEscapeRadius (_, z, _, _) = magnitude z < r

printIteration (n, z, z2, z2PlusC) = do
    putStrLn $ "\nn :=      " ++ show n
    putStrLn $   "z =       " ++ show z
    putStrLn $   "z^2 =     " ++ show z2
    putStrLn $   "z^2 + c = " ++ show z2PlusC

This is what the output for these points looks like at the 123rd iteration:

• (1.2353312256782e-2, -1.4127067356406e-2)
• (1.2353312257859e-2, -1.4127067356414e-2)

> runhaskell DebugJuliaSet.hs -8.01030596311150589e-01 1.56495138793530941e-01 1.2353312256782e-2 -1.4127067356406e-2 2
...
n :=      123
z =       (-0.23523642439355696) :+ (-0.1401978675009405)
z^2 =     3.568073330965438e-2 :+ 6.595929011704581e-2
z^2 + c = (-0.7653498630014962) :+ 0.22245442891057676
...

> runhaskell DebugJuliaSet.hs -8.01030596311150589e-01 1.56495138793530941e-01 1.2353312257859e-2 -1.4127067356414e-2 2
...
n :=      123
z =       (-0.23523642439355696) :+ (-0.14019786750094054)
z^2 =     3.5680733309654364e-2 :+ 6.595929011704584e-2
z^2 + c = (-0.7653498630014962) :+ 0.22245442891057676
...

Once the numbers are equal, the algorithm takes the exact same execution path and the numbers pass the escape radius after the same amount of iterations. That is a crucial difference between this and the function of the Mandelbrot set. In the Julia set the pixel coordinate only impacts the initialization of the algorithm, while in the Mandelbrot set the pixel value impacts C, which is added in each iteration. So similar values are much more likely to take a different path and therefore different numbers of iterations to pass the escape radius.

The only way I can think of to work around this, is to use higher precision data types When rendering this fractal using C++ i tried __float128 and long double which in my case has 80Bits I guess. The program becomes much slower, but the artifacts only seem to apper at much deeper zooms.

Rendering with double in C++ - Center: (0, 0); Zoom: 17665391; Iterations: 2283

Rendering with long double in C++ - Center: (0, 0); Zoom: 17665391; Iterations: 2283

Rendering with long double in C++ - Center: (0, 0); Zoom: 879474690; Iterations: 2283

In your case this doesn't appear to work that well, your wrapper seems to be flawed. How exactly are you representing the values in your custom data type? Also maybe you could consider using Decimal from .NET:

I hope, things are a bit clearer for you now.