There's an array A containing (positive and negative) integers. Find a (contiguous) subarray whose elements' absolute sum is minimal, e.g.:
A = [2, -4, 6, -3, 9]
|(−4) + 6 + (−3)| = 1 <- minimal absolute sum
I've started by implementing a brute-force algorithm which was O(N^2) or O(N^3), though it produced correct results. But the task specifies:
complexity:
- expected worst-case time complexity is O(N*log(N))
- expected worst-case space complexity is O(N)
After some searching I thought that maybe Kadane's algorithm can be modified to fit this problem but I failed to do it.
My question is - is Kadane's algorithm the right way to go? If not, could you point me in the right direction (or name an algorithm that could help me here)? I don't want a ready-made code, I just need help in finding the right algorithm.
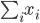 such as
such as