0

I am new to matlab, apologies if the question is silly. I am using the fmincon function to derive the elements of a 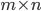m x n matrix (X) which will maximize the following objective function subject to the non-negativity constraint and:

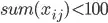
sum(x_{ij}) < 100

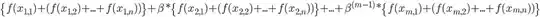
{f(x(1,1))+(f(x(1,2))+...+f(x(1,n))} + Beta*{f(x(2,1))+(f(x(2,2))+...+f(x(2,n))}+...+(Beta^(m-1))*{f(x(m,1))+(f(x(m,2))+...+f(x(m,n))}

where

f(xij)=zeta*[((alpha*pf*(xij^delta))-(pw*xij))^gamma]

In the code I used to do this fmincon was used, as the objective function is non-linear:

function optim = optim(m,n)
A= ones(1,m*n);
b = 100;
z = zeros(m,n);
in = inf(m,n);
X = ones(m,n);

[x, bestval] = fmincon(@myfun2,X,A,b,[],[],z,in,[])

  function f = myfun2(x)
  Alpha = 5;
  %kappa = 5;
  zeta = 5;
  beta = 0.90909;
  delta = 0.4;
  gamma = 0.4;
  pf = 1;
  pw = 1;

  for i= 1:m
     f=0;
     sum(i)=0;
        for j=1:n
        sum(i) = sum(i) +((beta^(i-1))*(-1)*(zeta)*(((Alpha*pf.*((x(i,j)).^delta))- 
                 (pw.*x(i,j)))^gamma));

         end
     f = f+sum(i)
   end

 end
end

When the code was run for a 5x5 matrix (optim(5,5)), the resulting solution was x =

1.5439    1.5439    1.5439    1.5439    1.5439
1.5439    1.5439    1.5439    1.5439    1.5439
1.5439    1.5439    1.5439    1.5439    1.5439
1.5439    1.5439    1.5439    1.5439    1.5439
3.1748    3.1748    3.1748    3.1748    3.1748


bestval =

-31.8780

But this is not a global minimum - as the marginal conditions specify at the global minimum we would have (for 1st row):

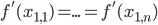
f'(x11)=...=f'(x1n)

And so on for each row. Also we would have for each column:

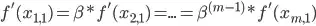
f'(x11)=beta*f'(x21)=...=(beta^m-1)*f'(xm1)

For the first column and so on. None of these conditions are satisfied by the resulting matrix. I have looked at the the related questions in stack overflow and also the documentation and I have no inkling of how to get better results. Is there a problem with the code? Can the code be tweaked to get better results?

Can I make the marginal conditions the stopping conditions and how could i go about doing that. or Can I use the Jacobian in some way? Any help would be appreciated. Thank You.

mkierc
  • 1,193
  • 2
  • 15
  • 28
uday kumar
  • 1
  • 1
  • If you have a non-convex minimization problem then you're not guaranteed that a gradient-based solver like `fmincon` will return the global optimal solution. Instead you might obtain a locally optimal solution. – josliber Sep 13 '14 at 02:15

1 Answers1

0

No optimization technique is guaranteed to return the global minimum. Some algorithms are guaranteed to find a local minimum if the Hessian is positive definite, however there is no mathematical way to determine only from the function values and its nth derivatives if a local minimum is the global minimum.

Now as for your termination conditions. You can pass in an options structure to fmincon, which has parameters to control the operation of fmincon. You can choose a different algorithm to best suit your problem. I would read the docs for this options structure, and see if anything there fits what you are trying to do.

http://www.mathworks.com/help/optim/ug/optimoptions.html

Karl
  • 315
  • 2
  • 9