You can try my latest lib Geometry3D by
pip install Geometry3D
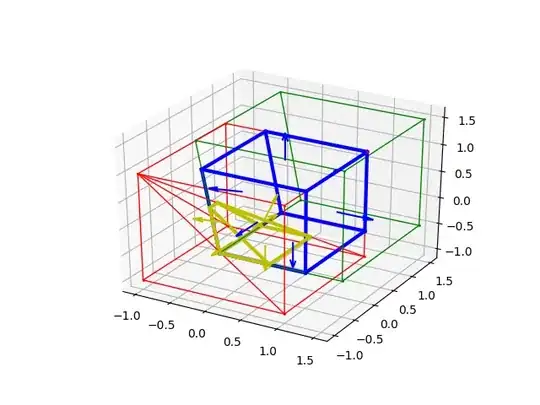
An example is shown below
>>> from Geometry3D import *
>>>
>>> a = Point(1,1,1)
>>> b = Point(-1,1,1)
>>> c = Point(-1,-1,1)
>>> d = Point(1,-1,1)
>>> e = Point(1,1,-1)
>>> f = Point(-1,1,-1)
>>> g = Point(-1,-1,-1)
>>> h = Point(1,-1,-1)
>>> cph0 = Parallelepiped(Point(-1,-1,-1),Vector(2,0,0),Vector(0,2,0),Vector(0,0,2))
>>> cpg12 = ConvexPolygon((e,c,h))
>>> cpg13 = ConvexPolygon((e,f,c))
>>> cpg14 = ConvexPolygon((c,f,g))
>>> cpg15 = ConvexPolygon((h,c,g))
>>> cpg16 = ConvexPolygon((h,g,f,e))
>>> cph1 = ConvexPolyhedron((cpg12,cpg13,cpg14,cpg15,cpg16))
>>> a1 = Point(1.5,1.5,1.5)
>>> b1 = Point(-0.5,1.5,1.5)
>>> c1 = Point(-0.5,-0.5,1.5)
>>> d1 = Point(1.5,-0.5,1.5)
>>> e1 = Point(1.5,1.5,-0.5)
>>> f1 = Point(-0.2,1.5,-0.5)
>>> g1 = Point(-0.2,-0.5,-0.5)
>>> h1 = Point(1.5,-0.5,-0.5)
>>>
>>> cpg6 = ConvexPolygon((a1,d1,h1,e1))
>>> cpg7 = ConvexPolygon((a1,e1,f1,b1))
>>> cpg8 = ConvexPolygon((c1,b1,f1,g1))
>>> cpg9 = ConvexPolygon((c1,g1,h1,d1))
>>> cpg10 = ConvexPolygon((a1,b1,c1,d1))
>>> cpg11 = ConvexPolygon((e1,h1,g1,f1))
>>> cph2 = ConvexPolyhedron((cpg6,cpg7,cpg8,cpg9,cpg10,cpg11))
>>> cph3 = intersection(cph0,cph2)
>>>
>>> cph4 = intersection(cph1,cph2)
>>> r = Renderer()
>>> r.add((cph0,'r',1),normal_length = 0)
>>> r.add((cph1,'r',1),normal_length = 0)
>>> r.add((cph2,'g',1),normal_length = 0)
>>> r.add((cph3,'b',3),normal_length = 0.5)
>>> r.add((cph4,'y',3),normal_length = 0.5)
>>> r.show()
You can also look at the documentation Geomrtry3D
