Just one more approach for solving the problem (for those who have uneasy time understanding it, like I have).
First.
Since we are talking about "the smaller of the two subarrays", then its length is less than 1/2 * n (n - the number of elements in original array).
Second.
If 0 < a < 0.5 it means the a * n is less than 1/2 * n either.
And thus we are talking from now about two randomly chosen integers bounded by 0 at lowest and 1/2 * n at highest.
Third.
Lets imagine the dice with numbers from 1 to 6 on it's sides. Lets choose a number from 1 to 6, for example 4. Now roll the dice. Each number has a probability 1/6 to be the outcome of this roll. Thus for event "outcome is less or equal to 4" we have probability equal to the sum of probabilities of each of this outcomes. And we have numbers 1, 2, 3 and 4. Altogether p(x <= 4) = 4 * 1/6 = 4/6 = 2/3. So the probability of event "output is bigger than 4" is p(x > 4) = 1 - p(x <= 4) = 1 - 2/3 = 1/3.
Fourth.
Lets go back to our problem. The "chosen number" is now a * n. And we are going to roll the dice with the numbers from 0 to (1/2 * n) on it to get k - the number of elements in a smallest of subarrays. The probability that outcome is bounded by (a * n) at highest is equals to sum of the probabilities of all outcomes from 0 to (a * n). And the probability for any particular outcome k is p(k) = 1 / (1/2 * n).
Therefore p(k <= a * n) = (a * n) * (1 / (1/2 * n)) = 2 * a.
From this we can easily conclude that p(k > a * n) = 1 - p(k <= a * n) = 1 - 2 * a.
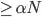 you can deduce that the pivot must also be in position
you can deduce that the pivot must also be in position 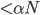 then there is a subarray smaller than
then there is a subarray smaller than 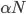 . By the same reasoning the pivot must also be
. By the same reasoning the pivot must also be 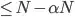 . Any larger value for the pivot will yield a smaller subarray than
. Any larger value for the pivot will yield a smaller subarray than 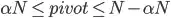 , as shown by the diagram below:
, as shown by the diagram below: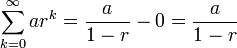
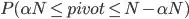 .
.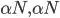 .
.