Wireframe shader - Issue with Barycentric coordinates when using shared vertices

Question

I'm working on drawing a terrain in WebGL. The problem is that I'm only using 4 vertices to draw a single quad by using indices to share vertices. So I can't upload unique baricentric coordinates for each vertex, because it's shared.

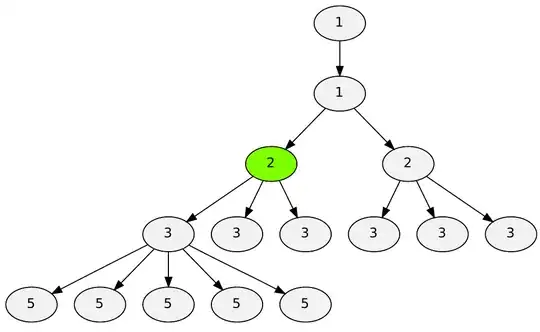
Here's a picture that shows the problem more clearly.

There's no barycentric coordinate that I can use for the question mark. (0,1,0) is used top left, (0,0,1) is used above and (1,0,0) is used to the left. So there's absolutely no way I can do this when I'm using indices to save vertex count.

Do I really save that much performance drawing a quad using 4 vertices instead of 6? If not then that's the easiest way to fix my problem. But I'm still curious if there's a way I can do it with shared vertices.

I'm aware that I can draw my terrain in wireframe using GL_LINES but I don't like that method, I want to have more control over my wireframe (e.g. not make it transparent).

Some people might ask why I'm using barycentric coordinates to draw my terrain in wireframe mode, it's because it works nicely in this demo:

http://codeflow.org/entries/2012/aug/02/easy-wireframe-display-with-barycentric-coordinates/

So it's basically two things I'm looking for:

• Do I lose much performance drawing my terrain where each quad is using 6 vertices instead of 4? Because if not, then that would solve my problem by not sharing vertices.
• Is it possible to have unique barycentric coordinate for 4 vertices that are shared to draw a single quad?

Thanks!

Answer 1

If you don't require to draw the diagonal of each quad in your wireframe, and are fine with only drawing the edges of each quad, this gets much simpler. There's no need to worry about barycentric coordinates if you operate on quads instead of triangles. Instead of the 3 barycentric coordinates, use 2 coordinates for the relative position within the mesh:

0,2----1,2----2,2----3,2----4,2
 |      |      |      |      |
 |      |      |      |      |
 |      |      |      |      |
0,1----1,1----2,1----3,1----4,1
 |      |      |      |      |
 |      |      |      |      |
 |      |      |      |      |
0,0----1,0----2,0----3,0----4,0

This also allows you to share vertices across quads, cutting the total number of vertices in your model by approximately a factor of 4.

You then feed these coordinate pairs from the vertex shader through to the fragment shader just like it's described for the barycentric coordinates in the article you linked.

In the fragment shader, the code gets just slightly more complicated, since it needs to test for values being either close to 0 or close to 1, after taking the fractional part. I haven't tested this, but it could look something like this, with vQC being the equivalent of vBC in the article:

varying vec2 vQC;
...
void main() {
    vec2 vRel = fract(vQC);
    if (any(lessThan(vec4(vRel, 1.0 - vRel), vec4(0.02)))) {
        gl_FragColor = vec4(0.0, 0.0, 0.0, 1.0);
    } else {
        gl_FragColor = vec4(0.5, 0.5, 0.5, 1.0);
    }
}

Answer 2

There are three barycentric coordinates (100, 010, and 001) I will denote HTO (for hundreds, tens, and ones, even though these are clearly not decimal numbers--this shorthand is for convenience). You want to submit these in this pattern:

O H T O H
T O H T O
H T O H T
O H T O H
T O H T O

You can see that for any triangle you start on, once you assign the three coordinates to it, its edges "choose" two coordinates for the surrounding triangle, leaving only one choice for each of those triangle's remaining vertex. Note that the tiling will mirror depending on where you're splitting the quads they make up (you'll always wind up with the far corners of each triangle in a quad having the same vertex, like the two Os in that first TOH-THO in the two in the lower left).

Whether you're feeding in indexed vertices or triangle strips, you'll have to supply your barycentric coordinates in the same order as the vertex they belong to. So, for a strip one high by two wide:

verts = [ A B C D E F ];
barycentric = [ T O H O H T ];
indices = [ 0 1 4 0 4 3 1 2 5 1 5 4 ];

Here's a simple algorithm for assigning coordinates:

barycentricTiles = [[1,0,0],[0,1,0],[0,0,1]];
// looping where i, j are indexes for each point on your mesh from 0,0 to m,n
barycentric.push(barycentricTiles[ (i+j)%3 ]);

I spent some time last week figuring this out, so I thought I'd pass it on. Sorry it's three years too late!

Answer 3

I would create my mesh using quads of two triangles, where vertices are not shared between adjacent quads. This will result in a larger mesh (around 4x), but the render performance will most likely be more efficient due to better data locality in the memory layout.