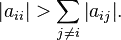Jacobi iteration doesn't end

Question

I'm trying to implement the Jacobi iteration in MATLAB but am unable to get it to converge. I have looked online and elsewhere for working code for comparison but am unable to find any that is something similar to my code and still works. Here is what I have:

function x = Jacobi(A,b,tol,maxiter)

n = size(A,1);
xp = zeros(n,1); 
x = zeros(n,1); 
k=0; % number of steps

while(k<=maxiter)
    k=k+1;

    for i=1:n
       xp(i) = 1/A(i,i)*(b(i) - A(i,1:i-1)*x(1:i-1) - A(i,i+1:n)*x(i+1:n));
    end

    err = norm(A*xp-b);

    if(err<tol)
        x=xp;
        break;
    end

    x=xp;

end

This just blows up no matter what A and b I use. It's probably a small error I'm overlooking but I would be very grateful if anyone could explain what's wrong because this should be correct but is not so in practice.

Answer 1

Your code is correct. The reason why it may not seem to work is because you are specifying systems that may not converge when you are using Jacobi iterations.

To be specific (thanks to @Saraubh), this method will converge if your matrix A is strictly diagonally dominant. In other words, for each row i in your matrix, the absolute summation of all of the columns j at row i without the diagonal coefficient at i must be less than the diagonal itself. In other words:

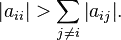
However, there are some systems that will converge with Jacobi, even if this condition isn't satisfied, but you should use this as a general rule before trying to use Jacobi for your system. It's actually more stable if you use Gauss-Seidel. The only difference is that you are re-using the solution of x and feeding it into the other variables as you progress down the rows. To make this Gauss-Seidel, all you have to do is change one character within your for loop. Change it from this:

xp(i) = 1/A(i,i)*(b(i) - A(i,1:i-1)*x(1:i-1) - A(i,i+1:n)*x(i+1:n));

To this:

xp(i) = 1/A(i,i)*(b(i) - A(i,1:i-1)*xp(1:i-1) - A(i,i+1:n)*x(i+1:n));
                                    **HERE**

Here are two examples that I will show you:

1. Where we specify a system that does not converge by Jacobi, but there is a solution. This system is not diagonally dominant.
2. Where we specify a system that does converge by Jacobi. Specifically, this system is diagonally dominant.

---

Example #1

A = [1 2 2 3; -1 4 2 7; 3 1 6 0; 1 0 3 4];
b = [0;1;-1;2];
x = Jacobi(A, b, 0.001, 40)
xtrue = A \ b

x =

1.0e+09 *

4.1567
0.8382
1.2380
1.0983

xtrue =

-0.1979
-0.7187
 0.0521
 0.5104

Now, if I used the Gauss-Seidel solution, this is what I get:

x =

-0.1988
-0.7190
0.0526
0.5103

Woah! It converged for Gauss-Seidel and not Jacobi, even though the system isn't diagonally dominant, I may have an explanation for that, and I'll provide later.

Example #2

A = [10 -1 2 0; -1 -11 -1 3; 2 -1 10 -1; 0 3 -1 8];
b = [6;25;-11;15];
x = Jacobi(A, b, 0.001, 40);
xtrue = A \ b

x =

0.6729
-1.5936
-1.1612
2.3275

xtrue =

0.6729
-1.5936
-1.1612
2.3274

This is what I get with Gauss-Seidel:

x =

0.6729
-1.5936
-1.1612
2.3274

This certainly converged for both, and the system is diagonally dominant.

---

As such, there is nothing wrong with your code. You are just specifying a system that can't be solved using Jacobi. It's better to use Gauss-Seidel for iterative methods that revolve around this kind of solving. The reason why is because you are immediately using information from the current iteration and spreading this to the rest of the variables. Jacobi does not do this, which is the reason why it diverges more quickly. For Jacobi, you can see that Example #1 failed to converge, while Example #2 did. Gauss-Seidel converged for both. In fact, when they both converge, they're quite close to the true solution.

Again, you need to make sure that your systems are diagonally dominant so you are guaranteed to have convergence. Not enforcing this rule... well... you'll be taking a risk as it may or may not converge.

Good luck!

Answer 2

Though this does not point out the problem in your code, I believe that you are looking for the Numerical Methods: Jacobi File Exchange Submission.

%JACOBI   Jacobi iteration for solving a linear system.
% Sample call
%   [X,dX] = jacobi(A,B,P,delta,max1)
%   [X,dX,Z] = jacobi(A,B,P,delta,max1)

It seems to do exactly what you describe.

Answer 3

As others have pointed out that not all systems are convergent using Jacobi method, but they do not point out why? Actually only a small sub-set of systems converge with Jacobi method.

The convergence criteria is that the "sum of all the coefficients (non-diagonal) in a row" must be lesser than the "coefficient at the diagonal position in that row". This criteria must be satisfied by all the rows. You can read more at: Jacobi Method Convergence

Before you decide to use Jacobi method, you must see whether this criteria is satisfied by the numerical method or not. The Gauss-Seidel method has a slightly more relaxed convergence criteria which allows you to use it for most of the Finite Difference type numerical methods.