Solving symbolic equation in matlab

Question

I am trying to solve a symbolic equation of the form

D = lamda^12/339288145381785600000 + lamda^10/18124366740480000 +
    lamda^8/7846046208000 + lamda^6/523908000 + lamda^4/25200

where lamda is declared as sym. The output I get is not in a readable form. Even vpa is not giving me the answer in readable form. what can be the solution?

See [**this**](http://www.wolframalpha.com/input/?i=a%5E12%2F339288145381785600000+%2B+a%5E10%2F18124366740480000+%2B+a%5E8%2F7846046208000+%2B+a%5E6%2F523908000+%2B+a%5E4%2F25200) for some help about your formula. — Sifu, Jul 11 '14 at 12:40
It's unclear what you're trying to do - show how you're trying to solve this equation (`solve`, `vpasolve`, etc) what output you get that isn't "readable", and what kind of output you expect/want. — nkjt, Jul 11 '14 at 13:31
I allways reccomend to use mupad for symbolic operations. Works pretty nice — Ander Biguri, Jul 11 '14 at 15:15

score 2 · Answer 1 · answered Jul 12 '14 at 00:32

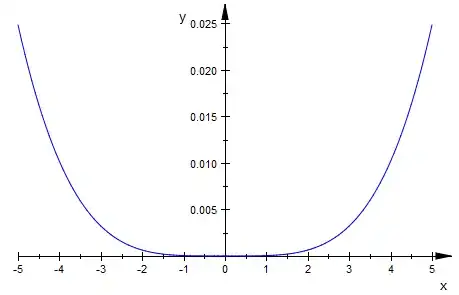
First we define the symbolic function:

syms x
f(x) = x^12/339288145381785600000 + x^10/18124366740480000 + ...
    x^8/7846046208000 + x^6/523908000 + x^4/25200;
ezplot(f)

equation function_plot

Next we find the roots (by solving it numerically). You could also use the vpasolve MATLAB function:

sol = feval(symengine, 'numeric::solve', f==0, x)

There is 1 real solution and 8 complex ones:

>> sol(:)
sol =
   79.624598247213536847657202795915 - 49.037140566365604310129811798328*i
   79.624598247213536847657202795915 + 49.037140566365604310129811798328*i
                                       118.88396448746822093664197370373*i
                                      -118.88396448746822093664197370373*i
                                      -111.61305465738189638915837157361*i
                                       111.61305465738189638915837157361*i
                                                                         0
 - 79.624598247213536847657202795915 - 49.037140566365604310129811798328*i
 - 79.624598247213536847657202795915 + 49.037140566365604310129811798328*i

Finally we plot the roots:

s = double(sol);
plot(real(s), imag(s), 'r.', 'MarkerSize',25)
axis square; axis([-100 100 -150 150]); box on
line(xlim(), [0 0], 'Color','k', 'LineStyle',':')
line([0 0], ylim(), 'Color','k', 'LineStyle',':')
xlabel('Re(x)'), ylabel('Im(x)'), title('Roots in Complex Plane')

roots_complex_plane

Solving symbolic equation in matlab

1 Answers1