Line of symmetry for an object in an image

Question

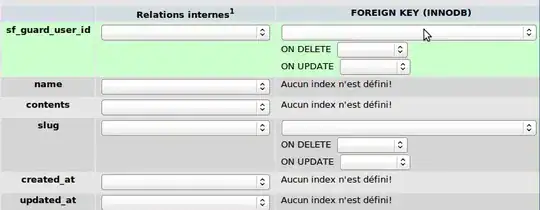
I wish to find the line of symmetry (LOS) for the object in this image (link below) and align the image so that the LOS is vertical.The object isn't perfectly symmetrical.

I'm working with c#,using aforge.net for image processing. The output I'm looking for is this:

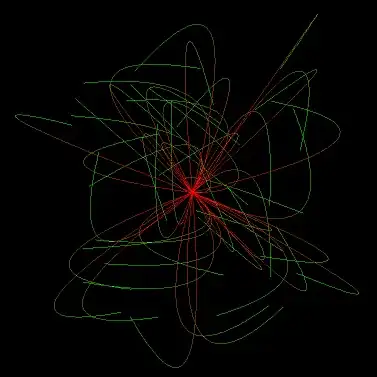
I've tried determining two diameters by drawing tangents in the x & y directions (find the image in the comment below) and found a center from their point of intersection.

I'm stuck at this point not knowing how to proceed..any help would be greatly appreciated,thank you!

Answer 1

For detecting symmetrie I can recommend the answer of this post: A distance measure to find similarity between two images invariant of transformation(Rotation & scaling) Intensity difference. It was used for detecting symmetrie on a facade. The problem I see is that your symmetrie line is not orthogonal. But maybe you can handle this problem by rotating the image or rotating the line of the symmetrie.

Approach one is to rotate the line for symmetrie computation for the two area. The angle of the line with the best Kullback-Leibler distance is your rotation angle.

And approach two is to have the line for area splitting and symmetrie detection fix and rotate the image around his center. The angle with the best Kullback-Leibler distance is your final angle. I think the c# will help you with this approach and this is the easier way.

Answer 2

You can try by computing the inertia tensor of the white pixels (sums of X², XY and Y², after centering). The Eigenvectors will give you the rotation angle.

For this to work, anyway, the shape must be asymmetric around the other axis, as regards inertia.