Here is latest version that produce effect close to the desired
void DeleteFrequencies(short *audioDataBuffer, const int bufferSize, int lowestFrequency, int highestFrequency, int sampleRate )
{
int frequencyInHzPerSample = sampleRate / bufferSize;
/* __________________________
/* ___________ __________________________ filter kernel */
int nOfPointsInFilterKernel = (lowestFrequency / frequencyInHzPerSample) + ( bufferSize - highestFrequency / frequencyInHzPerSample);
U u;
double *RealX = new double[bufferSize];
double *ImmX = new double[bufferSize];
ShortArrayToDoubleArray(audioDataBuffer, RealX, bufferSize);
// padd with zeroes, so that inputSignalSamplesNumber + kernelLength - 1 = bufferSize
// convert to frequency domain
ForwardRealFFT(RealX, ImmX, bufferSize);
// cut frequences < 300 && > 3400
int Multiplyer = 1;
for (int i = 0; i < 512; ++i)
{
if (i * 8000 / 1024 > 3400 || i * 8000 / bufferSize < 300 )
{
RealX[i] = 0;
ImmX[i] = 0;
}
if (i < lowestFrequency / frequencyInHzPerSample || i > highestFrequency / frequencyInHzPerSample )
Multiplyer = 0;
else
Multiplyer = 1;
RealX[i] = RealX[i] * Multiplyer /*ReH[f]*/ - ImmX[i] * Multiplyer;
ImmX[i] = ImmX[i] * Multiplyer + RealX[i] * Multiplyer;
}
ReverseRealFFT(RealX, ImmX, bufferSize);
DoubleArrayToShortArray(RealX, audioDataBuffer, bufferSize);
delete [] RealX;
delete [] ImmX;
}
but why it works this way???
Important that I just started learning DSP, so I can be unaware of some important ideas
(i appologise for that, but I have task which I need to solve: i need to reduce background noise in the recorder speeach, I try to approach that by cuting off from recorded speech frequencies in ranges <300 && > 3700 (as human voice in [300;3700] range) I started from that method as it is simple, but I found
out - it can`t be applied (please see - https://dsp.stackexchange.com/questions/6220/why-is-it-a-bad-idea-to-filter-by-zeroing-out-fft-bins/6224#6224 - thanks to @SleuthEye for reference).
So can you please suggest me simple solution based on the FFT usage that will allow me at least remove given ranges of frequneces?
I am trying to implement ideal band pass filter. But it isn't working as I expect - only high frequencies are cut.
Here is my implementation description:
- Read ampiltude values from PCM (raw) 16 bit format with sampling rate 8000 hz to the buffer of shorts of size 1024
- Apply FFT to go from time domain to the frequency domain
- Zero all frequencies < 300 and > 3700:
- Inverse FFT
union U
{
char ch[2];
short sh;
};
std::fstream in;
std::fstream out;
short audioDataBuffer[1024];
in.open ("mySound.pcm", std::ios::in | std::ios::binary);
out.open("mySoundFilteres.pcm", std::ios::out | std::ios::binary);
int i = 0;
bool isDataInBuffer = true;
U u;
while (in.good())
{
int j = 0;
for (int i = 0; i < 1024 * 2; i+=2)
{
if (false == in.good() && j < 1024) // padd with zeroes
{
audioDataBuffer[j] = 0;
}
in.read((char*)&audioDataBuffer[j], 2);
cout << audioDataBuffer[j];
++j;
}
// Algorithm
double RealX [1024] = {0};
double ImmX [1024] = {0};
ShortArrayToDoubleArray(audioDataBuffer, RealX, 1024);
// convert to frequency domain
ForwardRealFFT(RealX, ImmX, 1024);
// cut frequences < 300 && > 3400
for (int i = 0; i < 512; ++i)
{
if (i * 8000 / 1024 > 3400 || i * 8000 / 1024 < 300 )
{
RealX[i] = 0;
ImmX[i] = 0;
}
}
ReverseRealFFT(RealX, ImmX, 1024);
DoubleArrayToShortArray(RealX, audioDataBuffer, 1024);
for (int i = 0; i < 1024; ++i) // 7 6 5 4 3 2 1 0 - byte order hence we write ch[1] then ch[0]
{
u.sh = audioDataBuffer[i];
out.write(&u.ch[1], 1);
out.write(&u.ch[0], 1);
}
}
in.close();
out.close();
when I write result to a file, open it audacity and check spectr analysis, and see that high frequences are cut, but low still remains (they starts from 0)
What I am doing wrong?
Here is sound frequency spectr before 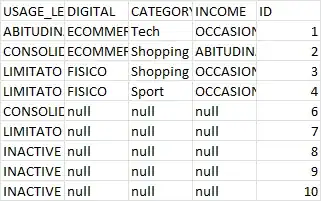
Here is sound frequency after I zeroed needed values 
Please help!
Update:
Here is code I came up with, what I should padd with Zeroes???
void DeleteFrequencies(short *audioDataBuffer, const int bufferSize, int lowestFrequency, int highestFrequency, int sampleRate )
{
// FFT must be the same length as output segment - to prevent circular convultion
//
int frequencyInHzPerSample = sampleRate / bufferSize;
/* __________________________
/* ___________ __________________________ filter kernel */
int nOfPointsInFilterKernel = (lowestFrequency / frequencyInHzPerSample) + ( bufferSize - highestFrequency / frequencyInHzPerSample);
U u;
double *RealX = new double[bufferSize];
double *ImmX = new double[bufferSize];
ShortArrayToDoubleArray(audioDataBuffer, RealX, bufferSize);
// padd with zeroes, so that inputSignalSamplesNumber + kernelLength - 1 = bufferSize
// convert to frequency domain
ForwardRealFFT(RealX, ImmX, bufferSize);
// cut frequences < 300 && > 3400
int Multiplyer = 1;
for (int i = 0; i < 512; ++i)
{
/*if (i * 8000 / 1024 > 3400 || i * 8000 / bufferSize < 300 )
{
RealX[i] = 0;
ImmX[i] = 0;
}*/
if (i < lowestFrequency / frequencyInHzPerSample || i > highestFrequency / frequencyInHzPerSample )
Multiplyer = 0;
else
Multiplyer = 1;
RealX[i] = RealX[i] * Multiplyer /*ReH[f]*/ - ImmX[i] * Multiplyer;
ImmX[i] = ImmX[i] * Multiplyer + RealX[i] * Multiplyer;
}
ReverseRealFFT(RealX, ImmX, bufferSize);
DoubleArrayToShortArray(RealX, audioDataBuffer, bufferSize);
delete [] RealX;
delete [] ImmX;
}
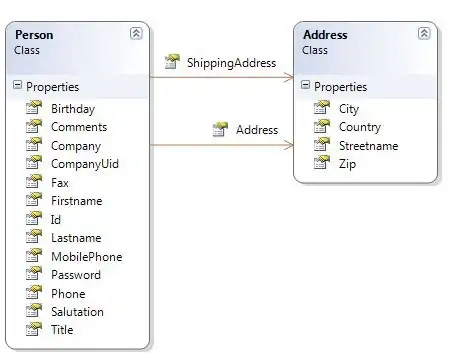
it produce the following spectrum (low frequencies are cut, but high not)
void ForwardRealFFT(double* RealX, double* ImmX, int nOfSamples)
{
short nh, i, j, nMinus1, nDiv2, nDiv4Minus1, im, ip, ip2, ipm, nOfCompositionSteps, LE, LE2, jm1;
double ur, ui, sr, si, tr, ti;
// Step 1 : separate even from odd points
nh = nOfSamples / 2 - 1;
for (i = 0; i <= nh; ++i)
{
RealX[i] = RealX[2*i];
ImmX[i] = RealX[2*i + 1];
}
// Step 2: calculate nOfSamples/2 points using complex FFT
// advantage in efficiency, as nOfSamples/2 requires 1/2 of the time as nOfSamples point FFT
nOfSamples /= 2;
ForwardDiscreteFT(RealX, ImmX, nOfSamples );
nOfSamples *= 2;
// Step 3: even/odd frequency domain decomposition
nMinus1 = nOfSamples - 1;
nDiv2 = nOfSamples / 2;
nDiv4Minus1 = nOfSamples / 4 - 1;
for (i = 1; i <= nDiv4Minus1; ++i)
{
im = nDiv2 - i;
ip2 = i + nDiv2;
ipm = im + nDiv2;
RealX[ip2] = (ImmX[i] + ImmX[im]) / 2;
RealX[ipm] = RealX[ip2];
ImmX[ip2] = -(RealX[i] - RealX[im]) / 2;
ImmX[ipm] = - ImmX[ip2];
RealX[i] = (RealX[i] + RealX[im]) / 2;
RealX[im] = RealX[i];
ImmX[i] = (ImmX[i] - ImmX[im]) / 2;
ImmX[im] = - ImmX[i];
}
RealX[nOfSamples * 3 / 4] = ImmX[nOfSamples / 4];
RealX[nDiv2] = ImmX[0];
ImmX[nOfSamples * 3 / 4] = 0;
ImmX[nDiv2] = 0;
ImmX[nOfSamples / 4] = 0;
ImmX[0] = 0;
// 3-rd step: combine the nOfSamples frequency spectra in the exact reverse order
// that the time domain decomposition took place
nOfCompositionSteps = log((double)nOfSamples) / log(2.0);
LE = pow(2.0,nOfCompositionSteps);
LE2 = LE / 2;
ur = 1;
ui = 0;
sr = cos(M_PI/LE2);
si = -sin(M_PI/LE2);
for (j = 1; j <= LE2; ++j)
{
jm1 = j - 1;
for (i = jm1; i <= nMinus1; i += LE)
{
ip = i + LE2;
tr = RealX[ip] * ur - ImmX[ip] * ui;
ti = RealX[ip] * ui + ImmX[ip] * ur;
RealX[ip] = RealX[i] - tr;
ImmX[ip] = ImmX[i] - ti;
RealX[i] = RealX[i] + tr;
ImmX[i] = ImmX[i] + ti;
}
tr = ur;
ur = tr * sr - ui * si;
ui = tr * si + ui * sr;
}
}