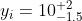How to calculate errors on slopes of linear fits when y-errors are asymmetric

Question

I have a data set with values that can be plotted as x-values against y-values. Data on the y-axis have asymmetric errors, i.e.,

I want to fit these data with a linear function. I can do this fit in a number of way in python, but all of them have the same problem, that is, how to get the errors of the fit parameters too.

Very related to this, but impossible (or at least, not straightforward) to use scipy.optimize.curve_fit since my data have asymmetric errors on the ordinate (y-axis) in order to get the slope error as well.

Then, how can I calculate errors on slopes of linear fits when y-error bars are asymmetric?

Is there any python function for this?

Answer 1

There's a paper by Barlow+04 https://arxiv.org/abs/physics/0406120 on finding the mean of variables with asymmetric error bars. You could perhaps use these techniques.

The brute force route that I take is to draw many realisations of the variable from a split-normal distribution (https://en.wikipedia.org/wiki/Split_normal_distribution) and store the best-fitting polynomial parameters for them. I then compute the median and 1-sigma upper/lower error bars (from the 84th and 16th percentile from the median, respectively) for each polynomial parameter.

The code below, in Python 2.7.9, does this. There's a function for computing a split-normal value, the errors from the percentiles and fitting a polynomial.

Hope this helps.

#! /bin/python

from random import choice, gauss
from numpy import polyfit

def split_normal(mus, sigmas_u68, sigmas_l68):
    """
    RET: A split-normal value.
    """

    split_normal = []

    for mu, sigma_u68, sigma_l68 in zip(mus, sigmas_u68, sigmas_l68):

        sigma = choice([sigma_u68, -sigma_l68])
        g = abs(gauss(0.0, 1.0)) * sigma + mu
        split_normal.append(g)

    return split_normal

def errors_84_16(x):
    """
    RET: 1-sigma upper/lower error bars from the 84/16th percentile
         from the median.
    """

    n = len(x)

    index_med = n / 2 # median.
    index_84 = int(round(n * 0.84135)) # 84th percentile from median.
    index_16 = int(round(n * 0.15865))

    x_sorted = sorted(x)
    x_med = x_sorted[index_med]
    x_u68 = x_sorted[index_84] - x_med # 1-sigma upper error.
    x_l68 = x_med - x_sorted[index_16] # 1-sigma lower error.

    return x_med, x_u68, x_l68

def assymetric_polyfit(x, y, y_u68, y_l68, n_mc=500):
    """
    DES: Solves y = a + b * x for assymentric y error bars.
    RET: [a, a_u68, a_l68, b, b_u68, b_l68].
    """

    a_mc = []
    b_mc = []

    for i in xrange(0, n_mc):
        y_mc = split_normal(y, y_u68, y_l68)
        pars = polyfit(x, y_mc, 2)
        a_mc.append(pars[2])
        b_mc.append(pars[1])


    a, a_u68, a_l68 = errors_84_16(a_mc)
    b, b_u68, b_l68 = errors_84_16(b_mc)

    return a, a_u68, a_l68, b, b_u68, b_l68

def example():
    """
    """

    x = [1.0, 2.0, 3.0, 4.0, 5.0]
    y = [5.0, 8.0, 11.0, 14.0, 17.0] # 2 + 3x
    y_u68 = [0.5, 0.5, 0.5, 0.5, 0.5]
    y_l68 = [1.5, 1.5, 1.5, 1.5, 1.5]

    pars = assymetric_polyfit(x, y, y_u68, y_l68)
    print(pars)

if __name__ == '__main__':

    example()