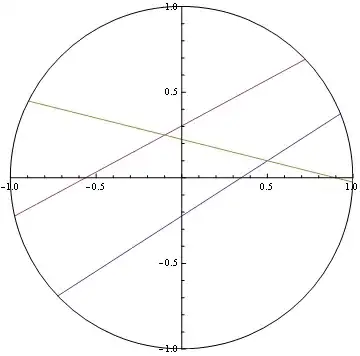
Two profile samples that are going to be fed to a 3d reconstruction system look as follows

Take X derivate + split red channel + threshold + DP onto nonzero pixels + connect DP points with lines result in:
I define my keypoints as:
i.e. any pixel from the first-big-bump, close to the ending
and the first-big-corner that is close to the lower part of deep arc.
How can I locate them programmatically using the resultant vector of white pixels ?
It is acceptable to modify the sample images to create your own noiseless ones.
It is acceptable to modify the pre-processing step.
No need for a generic and agressive solution, I am concerned just for these two.
I am hoping for ideas, instead of scripts/codes.
Thanks in advance
