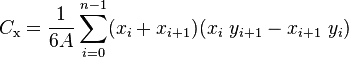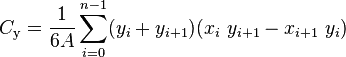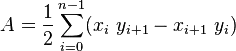Compute the centroid of a 3D planar polygon

Question

This is a similar question to this one here.

Given a list of 3D coordinates that define the surface( Point3D1, Point3D2, Point3D3, and so on), how to calculate the centroid of the surface?

In 2D the computation is given by the following formula:

alt text

What about the 3D analogue?

Area and centroid are very different things. Which do you want? — kennytm, Mar 01 '10 at 13:05
Just how do these points *define* the surface? If all the points are on the boundary of the surface (as all answers assumed so far), and they are not necessarily all in the same plane, the surface is not defined. If they define a triangulation, it's a whole different story. Or maybe you only have a point cloud? What is it? — AVB, Mar 01 '10 at 15:20
@AB: All the points must define the surface; they must be located at the same plane. This is the assumption. — Graviton, Mar 02 '10 at 01:03

tom10 · Answer 1 · 2010-03-03T13:06:01.790

10

Just use the equations that you have twice, but the second time swap in z for y.

That is, calculate the centroids of the two projections, one onto the x-y plane, and the other onto the x-z plane. The centroids of the projections will be projections of the actual centroid, so the answer will be the x, y, and z values you find from these two calculations.

Stated more explicitly: If your points are (x1, y1, z1), (x2, y2, z2),... , to get the x-y centroid, (Cx, Cy), do a calculation using (x1, y1), (x2, y2),... and to get the x-z centroid, (Cx, Cz) use the points (x1, z1), (x2, z2),.... -- just do the second calculation with your same 2D formula, treating the z values as the y in the equation. Then your 3D centroid will be (Cx, Cy, Cz). This will work as long as your surface is flat and isn't parallel to the x-y, x-z, or y-z planes (but if it is parallel it's just the 2D equation).

edited Mar 03 '10 at 13:06

answered Mar 02 '10 at 02:17

tom10

67,082
10
127
137

@tom10, can be more explicit about this? – Graviton Mar 02 '10 at 14:21
OK, added a paragraph giving a more explicit description. Does is say what you need to know? – tom10 Mar 02 '10 at 16:07
@tom10, in that case there are two sets of `Cx`. Which one to choose? Or we just pick the average? – Graviton Mar 04 '10 at 06:25
Both calculations of Cx should give the same result. – tom10 Mar 05 '10 at 15:40

kennytm · Answer 2 · 2010-03-01T13:31:51.210

5

Let the points be v₀, v₁, ..., v_N in counterclockwise, where v_i = (x_i, y_i, z_i).

Then the triplets (v₀, v₁, v₂), (v₀, v₂, v₃), ..., (v₀, v_i, v_i+1), ..., (v₀, v_N-1, v_N) forms N-1 triangles that create the polygon.

The area of each triangle is | (v_i − v₀) × (v_i+1 − v₀) | ÷ 2, where × is the cross product and | · | is vector length.

You may need to make the area negative to compensate for concave parts. A simple check is to compute (v_i − v₀) × (v_i+1 − v₀) · (v₁ − v₀) × (v₂ − v₀). The area should have the same sign as the result.

Since ratio of area of 2D figures is constant under parallel projection, you may want to choose a unit vector (e.g. z) not parallel to the plane, the treat (v_i − v₀) × (v_i+1 − v₀) · z as the area. With this, you don't need to perform the expensive square root, and the sign check is automatically taken care of.

The centroid of each triangle is (v₀ + v_i + v_i+1) ÷ 3.

Hence, the centroid of the whole polygon is, assuming uniform density,

                1       N-1
centroid = ——————————    ∑  ( centroid-of-triangle-i × area-of-triangle-i )
           total-area   i=1

(For dimensions ≥ 4D, the area needs to be computed with A_i = ½ |v_i−v₀| |v_i+1−v₀| sin θ_i, where cos θ_i = (v_i−v₀) · (v_i+1−v₀). )

edited Mar 01 '10 at 13:31

answered Mar 01 '10 at 13:21

kennytm

510,854
105
1,084
1,005

**Since ratio of area of 2D figures is constant under parallel projection, you may want to choose a unit vector (e.g. z) not parallel to the plane, the treat (vi − v0) × (vi+1 − v0) · z as the area**. Can be more explicit on that part? – Graviton Mar 01 '10 at 13:51
Take z = (v1-v0) × (v2-v0), for example. – AVB Mar 02 '10 at 02:15
@KennyTM, I think your formulation is good. But is there anyway to eliminate the special dependencies on the `v0`? Much like how the above 2D centroid computation is formulated. I'm sure with some tweaking it's possible to do it. – Graviton Mar 04 '10 at 02:03
@Ngu: Any v0 is fine. Or you could use tom10's solution (http://stackoverflow.com/questions/2355931/compute-the-centroid-of-a-3d-planar-polygon/2360507#2360507) – kennytm Mar 04 '10 at 06:22
@KennyTM, what I mean is, I don't want any `v0` or other subscript ( such as 1,2,3) to appear in my euqation. Or, to put it other way, the equation must involve only `vi`, `vi+1`, `vi-1` etc. No special `v0`, `v1` or `v2`. Is it possible to construct such an equation? – Graviton Mar 04 '10 at 06:27
@KennyTM, any special treatment of any special coordinate points seems not general enough to me. – Graviton Mar 04 '10 at 07:13
@Ngu: This is completely general. v0 can be chosen to be any vertex. – kennytm Mar 04 '10 at 07:25
@Kenny, there is another thing that worries me in your formulation, namely, you are doing this `| (vi − v0) × (vi+1 − v0) | ÷ 2` and later check for the concavity, are you saying that if the area is concave we should minus it out? – Graviton Mar 04 '10 at 07:35
@Ngu: Yes. If you're sure the polygon doesn't parallel to the z-axis you can use `(vi − v0) × (vi+1 − v0) · z` also, and it's much more efficient. – kennytm Mar 04 '10 at 07:38
Will this work for the concave polygon as well? – Avi Dec 01 '20 at 20:10

score 3 · Accepted Answer · answered Mar 01 '10 at 13:09

3

If it's a planar surface, you can transform to a coordinate system local to the plane, calculate the centroid using the formulas you presented, and then transform back to get its coordinates in 3D space.

answered Mar 01 '10 at 13:09

duffymo

305,152
44
369
561

1

Besides coordinate transformation, is there a direct method? If no, I would appreciate a formula on how to transform coordinate. – Graviton Mar 01 '10 at 13:11

Compute the centroid of a 3D planar polygon

3 Answers3

Linked