I wrote the following code to solve a system of 2 non-linear equations f[0] and f[1] in 2 unknowns th2 and th3:
from math import radians,degrees,sin,cos
from scipy import zeros
from scipy.optimize import fsolve
guess=[0,0]
th1=radians(30)
th4=radians(180)
l1=0.8
l2=3.9
l3=2.59
l4=4.
def residuals(x,th1,th4,l1,l2,l3,l4):
f=zeros(2)
th2=x[0]
th3=x[1]
f[0] = l1*cos(th1)+l2*cos(th2)+l3*cos(th3)+l4*cos(th4)
f[1] = l1*sin(th1)+l2*sin(th2)+l3*sin(th3)+l4*sin(th4)
return f
d=zeros(2)
c=fsolve(residuals,guess,args=(th1,th4,l1,l2,l3,l4))
This code is use to find th2 and th3 in the vectorial problem that you can see in the attached image:
Where the modules of the vectors r1, r2, r3 and r4 are the know quantities l1, l2, l3 and l4.
th1 is the angle of r1 in complex notation (polar coordinates, measured counter clockwise). th2, th3 and th4 are the angles of the polar coordinates of the vectors r2, r2 and r4.
The quantities th1 and th4 are know as you can see in the code.
th1 is an array of values that I will need to implement that includes all the possible values of the angle th1. I will implement the code that I wrote in a for cycle to generate th2 and th3 for The other know values are fixed values.
The problem of the actual code with the code is this: I am expecting two solutions for th2 and th3 for one given th1 because the vectors could be arranged in both the configurations that you can see in this image:
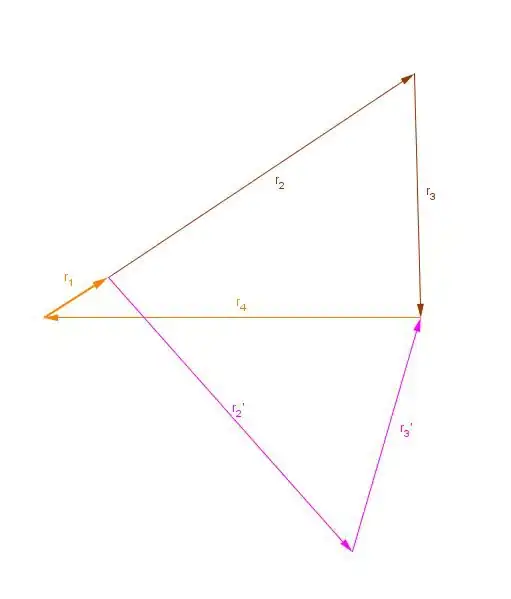
So I am expecting to get 2 solution for both th2 and th3. I am then interested only in the solutions where r2 and r3 do not cross r4. Unfortunately with the code that I wrote I get the "pink (crossed") solution sometimes and some other times the "brown" one.
I need help to:
1) Write code that will give me both the "pink" and the "brown" solution.
2) Write code that can take only the "brow" solution.