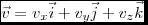Generate list of n (strictly positive) values such that the list has predetermined mean x and std. dev. y

Question

I would like to generate a list of n strictly positive values such that the list has a predetermined mean and standard deviation (can be close/not exact). I was using the uniform distribution's equations for expectation and variance and solving for 'a' and 'b', but the system of equations (for the specific mean and std. dev. I wanted) had no solutions for a, b >= 0. I was wondering if there was a plug-and-chug method to do this in any programming language, but hopefully in Python. Thanks!

Ex: generate list of 84 positive values with mean ~= 60/84 = 0.71, std.dev. ~= 1.7

Answer 1

Assume a (continuous) uniform distribution with the minimum a and the maximum b. Such distribution has the mean and variance:

mean = (a + b) / 2

var = (b - a)^2 / 12

where the standard deviation is simply sqrt(var). Given the mean and variance (and therefore standard deviation), the set of equations can be solved for a and b:

a = mean - sqrt(3 * var)

b = mean + sqrt(3 * var)

For creating a list having this set of mean and variance, you simply want to generate n equally separated points within [a, b]. A Python code snippet follows:

#!/usr/bin/env python2.7
from math import sqrt


def uniform(mean, std, n):
    a = mean - sqrt(3.) * std
    b = mean + sqrt(3.) * std
    xs = [(b - a) * (i / (n - 1.)) + a for i in range(n)]
    return xs


for target_mean, target_std, n in [(10, 1, 100),
                                   (0.71, 1.7, 84)]:
    xs = uniform(target_mean, target_std, n)
    print xs

    mean = 1. * sum(xs) / n
    var = sum([(x - mean)**2 / n for x in xs])

    print 'mean: {} ({})'.format(mean, target_mean)
    print 'std: {} ({})'.format(sqrt(var), target_std)

    if not min(xs) > 0:
        print 'WARNING: but this is not strictly positive'

    print

Note that a certain combination of mean and variance yields negative values, so you need to conditionally exclude them. You can alternatively choose some other probability distribution function that only draws strictly positive numbers. How easy it is to relate the mean and variance to the parameters that characterize the distribution really depends. I arbitrarily picked uniform because it is simple.

However, I find the premise of the original question a bit contrived, so depending on the problem doing this sort of thing might not actually be desirable.

Answer 2

Answer

Use NumPy to generate samples from a gamma distribution with scale parameter theta = variance / mean and shape parameter k = mean / theta.

Example

>> import numpy

>> mu = 0.71
>> var = 1.7**2 
>> theta = var / mean 
>> k = mu / theta

>> samples = numpy.random.gamma(k, theta, 1000)

>> numpy.mean(samples)
0.71622189354608201

>> numpy.std(samples) 
1.7865898752966483

Commentary

The constraints you provide underspecify the distribution. Some of the comments you made in response to another answer would have been helpful as part of the question. In particular, it seems as if you might be trying to model arrivals in a queue, e.g. a Poisson process. As you pointed out, the mean and variance of a Poisson distribution are the same, the lambda parameter. However, consider the lambda itself as a random variable. The conjugate prior to the Poisson distribution the Gamma distribution.

With shape parameter k > 0 and scale parameter theta > 0, the gamma distribution has mean = k * theta and variance = k * theta^2. Therefore, theta is variance / mean > 0 and k is mean / theta > 0. Since the gamma distribution has positive support, this conveniently answers your question.

Answer 3

The requirement for construction of distribution with given mean and deviation is impossible to be satisfied if deviation is greater than distance from mean to any bound. To see this let's first notice that in sample

x1, x2, ..., mean, ... , xn

with mean mi = sum(x_i)/n

deviation is bounded:

dev < xmax - mean, and dev < mean - xmin. Without providing formula it is quite intuitive since the meaning of it is average deviation from the mean - how could it be greater than the maximum deviation ( max of ( mean - xmin, xmax - mean)) from the mean?

So if deviation is greater than max of [ mean - xmin, xmax - mean] then we have error. Now let's take a look at two other cases:

• when it is in range (0, min of[ mean - xmin, xmax - mean])

• and when it is in range (0, max of[ mean - xmin, xmax - mean]) but not in range (0, min of[ mean - xmin, xmax - mean]), ( so it is greater than one bound, but less then other one)

---

When it is in range (0, min of[ mean - xmin, xmax - mean])

Bernoulli distribution

This is simple to construct some distribution that yields sample with mean mi and deviation d with all values in range [xmin, xmax]. The simple case of two points distribution with

x1 = mi - d, x2 = mi + d

has the expectation of mi and deviation of d.

#include <boost/random.hpp>
#include <boost/random/bernoulli_distribution.hpp>

double generate_from_bernoulli_distribution(double mi, double d,
                                                        double a, double b) {
    if (b <= a || d < 0) throw std::out_of_range( "invalid parameters");
    if (d > std::min(mi - a, b - mi)) throw std::out_of_range( " invalid
                                                         standard deviation");
    double x1 = mi - d, x2 = mi + d;
    boost::mt19937 rng; // I don't seed it on purpouse (it's not relevant)
    boost::bernoulli_distribution<> bd;
    boost::variate_generator<boost::mt19937&,
            boost::bernoulli_distribution<> > var_ber( rng, bd);
    double bernoulli = var_ber();
    return ( x1 + bernoulli * 2 * d); // return x1 on 0, or x2 on 1
}

void generate_n_from_bernoulli_distribution( double mi, double d, double a, 
                                   double b, std::vector<double>& res, int n) {
    if (b <= a || d < 0) throw std::out_of_range( "invalid parameters");
    if (d > std::min(mi - a, b - mi)) throw std::out_of_range( " invalid
                                                          standard deviation");
    double x1 = mi - d, x2 = mi + d;

    boost::mt19937 rng; // I don't seed it on purpouse (it's not relevant)
    boost::bernoulli_distribution<> bd;
    boost::variate_generator<boost::mt19937&,
            boost::bernoulli_distribution<> > var_ber( rng, bd);

    int i = 0;
    for (; i < n; ++i) {
        double bernoulli = var_ber();
        res.push_back( x1 + bernoulli * 2 * d); // push_back x1 on 0, or x2 on 1
    }
}

usage:

/*
 * 
 */
int main()
{
  double rc = generate_from_bernoulli_distribution( 4, 1, 0, 10);
  std::vector<double> sample;
  generate_n_from_bernoulli_distribution( 4, 1, 0, 10, sample, 100);
  return 0;
}

The case of Bernoulli, two points distribution is the first to consider as it has the weakest requirements. Sometimes it will be possible to draw also from other distributions, for example from uniform distribution.

---

Uniform distribution

The first two moments of uniform distribution (the mean and variance) in terms of its range [a, b] are given by

where

a = mi - alpha b = mi + alpha alpha is any real number

So there are infote number of uniform distributions that yield mean mi. All of them are just centered over mi. Additional requirement, for a variance gives us single solution for a, b:

/**
 * generates intervals for a uniform distribution
 * with a given mean and deviation
 * @param mi    mean
 * @param d     deviation
 * @param a     left bound
 * @param b     right bound
 * @return 
 */
void uniform_distribution_intervals( double mi, double d, double& a, double& b) {
    a = mi - d * std::sqrt(3.0);
    b = mi + d * std::sqrt(3.0);
}

It is clear that not always it is possible to find uniform distribution for a given mi, d, which will have left bound greater than 0. In this case

uniform_distribution_intervals( 60/84, 1.7, a, b);

unfortunately returns a = -2.9444863728670914, b = 2.9444863728670914.

---

when it is in range (0, max of[ mean - xmin, xmax - mean]) but not in range (0, min of[ mean - xmin, xmax - mean])

left as useful exercise

Answer 4

Saying a "distribution is unknown" is different than "does not really matter" (both statements are in the same comment to Taro Sato’s answer). One way to get a desired mean and standard deviation is to set M=mean+var^2/mean and have some samples barely positive and the other samples be M. By making the samples correctly, you’ll get the mean and standard deviation. In the case you listed: M=4.78, 12 samples of M, and 68 samples of .001 would give mean=.718 and std.dev.=1.71. But arrival times are not accurately modeled as some 0 and some M.