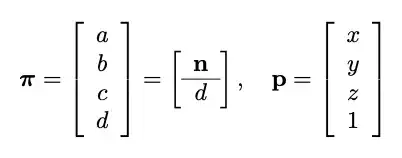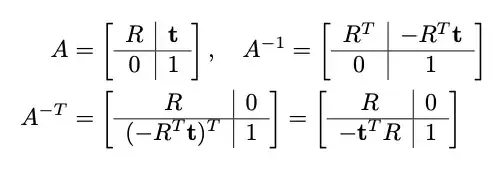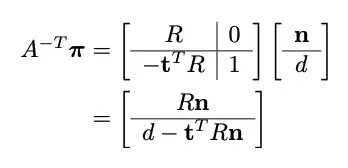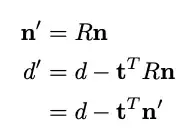How to efficiently rotate and translate a plane in 3D

Question

I have a plane defined by a normal (n) and a distance (d) (from the origin). I would like to transform it into a new system. The long way is like this: 1) multiply distance (d) with normal (n) resulting in a a vector (p) 2) rotate (R) and translate (v) the vector (p) to get (p') 3) normalize (p') to get the normal 4) use another algorithm to find the smallest distance (d') between the new plane and the origin

I haven't tried this but I guess it should work. QUestion: Isn't there a faster way to get n' and d'? If the translation (v) is 0 than I can skip 4). But if it is not 0? Is there an easier way to get the new d'?

score 6 · Accepted Answer · answered Feb 23 '10 at 09:39

You need to be careful because normals don't necessarily transform like points do, and the distance is the perpendicular distance to the origin, so you have to compute d'= d + n.v. If all you're doing is translation and rotation, then you can rotate the normal and compute a new perpendicular distance. But, if you're scaling your axes differently, or doing a general projective transformation, then you need to treat things differently.

The way that works for everything is to use homogeneous coordinates, so all your transforms are 4x4 matrices, and both your points and your planes are 4-vectors:

point p=(x,y,z)        -> homogeneous (x,y,z,1), equiv. to (x*W, y*W, z*W, W)
plane q=[n=(a,b,c), d] -> homogeneous [a,b,c,d], equiv. to [a*K, b*K, c*K, d*K)

  -> point p is on plane q iff:  p.q=0   (using homogeneous coords, as above)

Generally, you will multiply all your transformation matrices into one 4x4 matrix T, and use that matrix on every point, to determine its final transformed position. The trick is, you need to use the inverse transpose of T to transform your plane coordinates. From the following, you can see that this preserves incidence between points and planes:

point p' = T p
plane q' = (T^-1)^t q

  -> point p' is on plane q' when:  p'.q'=0

  then, note:  p'.q' = p^t T^t (T^-1)^t q = p^t q = p.q
  so:  p'.q'=0  whenever p.q=0

Yes I'm doing only rotation and translation. Somehow I was hoping to find a simple way to calculate the perpendicular distance based on the rotated normal or something. But then again, calculating the distance is it's not that costly. Thanks! — Golom, Feb 24 '10 at 19:14

score 1 · Answer 2 · answered Mar 02 '16 at 13:57

1

n' = n*R^T
d' = d - n*R^T*trans

answered Mar 02 '16 at 13:57

user3866289

131
1
2

2

Please add some comments about your solution on why and how it solves the problem – Bhavesh Odedra Mar 12 '16 at 08:48

score 1 · Answer 3 · answered Oct 12 '22 at 16:13

I am going to expand on the answers above in case folks want a few more details. Given the plane defined by its normal n = [a b c]^T and its distance d from the origin (assuming n has magnitude 1) and homogeneous point p

We can compute the signed Euclidean distance of p from the plane as follows

and note that if we transform p with an invertible transformation A then the distance of the transformed point is preserved if we transform the plane by the inverse transpose of A.

For the case where A is composed of a 3x3 rotation R and a 3x1 translation t we have

Thus we have

Therefore the new normal and d' are

How to efficiently rotate and translate a plane in 3D

3 Answers3

Linked