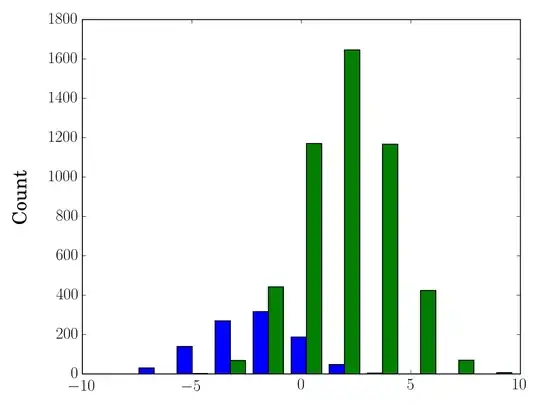
Is this a good way of plotting a Normal Distribution? On occasion, I get a pdf value (pdf_x) which is greater than 1.
% thresh_strain contains a Normally Distributed set of numbers
[mu_j,sigma_j] = normfit(thresh_strain);
x=linspace(mu_j-4*sigma_j,mu_j+4*sigma_j,200);
pdf_x = 1/sqrt(2*pi)/sigma_j*exp(-(x-mu_j).^2/(2*sigma_j^2));
plot(x,pdf_x);