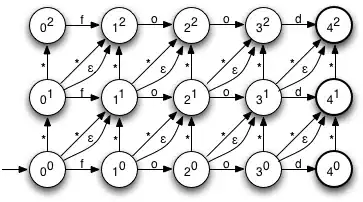
The use case is auto-complete options where I want to rank a large set of other strings by how like a fixed string they are.
Is there any bastardization of something like a DFA RegEx that can do a better job than the start over on each option solution?
The guy who asked this question seems to know of a solution but doesn't list any sources.
(p.s. "Read this link" type answer welcome.)