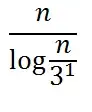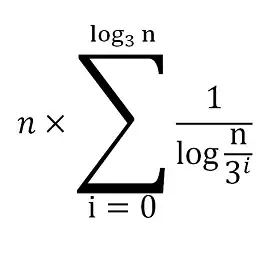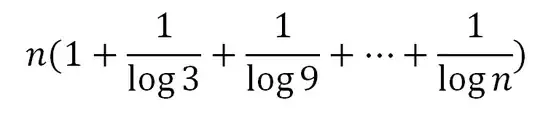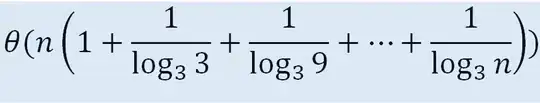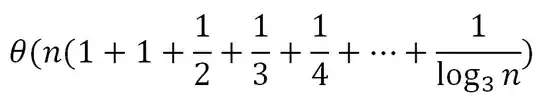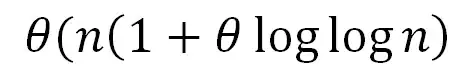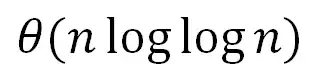8

Am trying to solve the given recursion, using recursion tree, T(n) = 3T(n/3) + n/lg n.

In the first level (n/3)/(log(n/3)) + (n/3)/(log(n/3)) + (n/3)/(log(n/3)) = n/(log(n/3)).

In the second level it turns out to be n/(log(n/9)).

Can I generalize the above equation in the form of n.loglogn

This is a general doubt I've, I need an insight on this.

Note: Any function that has to be Theta(n^k log^k (n)) in that function k should >=1. And in this case k is -1 so master theorem doesn't come in to picture

Chaitanya
  • 1,698
  • 5
  • 21
  • 41

3 Answers3

9

It is true, the Master theorem does not apply.

T(n) = 3T(n/3) + n/logn.

Let g(n) = T(n)/n.

Then ng(n) = 3(n/3)*g(n/3) + n/logn.

Thus

g(n) = g(n/3) + 1/log n.

This gives g(n) = Sum 1/log n + 1/log n/3 + 1/log n/9 + ...

= Theta(Sum 1/logn + 1/(logn -1) + 1/(log n - 2) + ...) = Theta(Integral 1/x between 1 and logn) = Theta(log log n).

Thus T(n) = ng(n) = Theta(nlog logn.)

You guessed it right.

  • Seems like there is an error right at the step between where you introduce g(n)=T(n)/n and the n*g(n)=... part; n/logn never went up to n^2/logn – Adam Miller Sep 12 '13 at 05:56
  • I am a little weak in calculus, can you please explain me how did you get from Sum 1/logn + 1/(logn-1) + 1/(logn-2) + ... to Integral 1/x between 1 and logn. I can understand that you are rewriting the infinite limit sum as an integral but I don't understand how. – logdev Aug 14 '19 at 14:24
5

If you use a tree to visualize the question, you'll see that the sum of each rank is:

  • rank 0:

enter image description here

(which is equal to n/log(n)) - rank 1:

enter image description here

and so forth, with a general sum of n/log(n/(3^i)) for each rank, i being the current rank. so, all together we get:

enter image description here

if we open the equation we get:

enter image description here

(starting from the end and going backwards.. first when i=log(base3)n and then going back)

since log base doesn't matter in theta, we get :

enter image description here

which is:

enter image description here

which is (in sigma):

enter image description here

which is a harmonic series, equal to:

enter image description here

and since ln is log with a base of e, and log bases don't matter in theta, we finally get:

enter image description here

which is equal to:

enter image description here

so, it's theta(n log log n).

josliber
  • 43,891
  • 12
  • 98
  • 133
shuminizer
  • 71
  • 1
  • 6
  • I actually fixed your links before opening them and now kinda regret it :P. Just stick the math in `code snippets` - it's more readable anyway. – Dan Scally Jun 25 '15 at 13:37
  • For anyone figuring out how harmonic series is approximated to log n checkout this [link](https://math.stackexchange.com/questions/496116/is-there-a-partial-sum-formula-for-the-harmonic-series) – logdev Aug 14 '19 at 15:06
1

T(n)=3T(⌊n3⌋)+2nlogn with base condition 1 when n<=1 By substitution method:

Answer page 1 Answer Page 1

Answer page 2 Answer page 2

J. M. Arnold
  • 6,261
  • 3
  • 20
  • 38
Kartik Khanna
  • 11
  • 2