plot the results glm with multiple explanatories with 95% CIs

Question

data:

df <- structure(list(x = c(9.5638945103927, 13.7767187698566, 6.0019477258207, 
10.1897072092089, 15.4019854273531, 10.9746646056535, 12.9429073949468, 
20.7513493525379, 18.5764146937149, 2.91302077116471, 13.6523222711501, 
10.0920467755108), y = c(83.949498880077, 18.066881289085, 71.3052196358606, 
39.8975644317452, 57.2933166677927, 87.8484256883889, 92.6818329896141, 
49.8297961197214, 56.3650103496898, 14.7950650020996, 37.9271392096266, 
50.4357237591891), z = c("a", "c", "e", "f", "b", "a", "b", "a", 
"b", "a", "c", "d")), .Names = c("x", "y", "z"), row.names = c(NA, 
-12L), class = "data.frame")

my model:

mod <- glm(y ~ x + I(x^2) + z, family=quasipoisson, data = df)
summary(mod)

I want to plot something like this:

ggplot(df, aes(x=x,y=y)) + 
  geom_point() +
  stat_smooth(method="lm",se=FALSE,
              formula=y~x+I(x^2),fill="transparent",
              colour="black") +
  stat_smooth(method="lm",geom="ribbon",
              formula=y~x+I(x^2),fill="transparent",
              colour="red",linetype="dashed",fullrange=TRUE) +
          scale_x_continuous(limits=c(-2,35)) +
          coord_cartesian(xlim=c(2,25),
                          ylim=range(pretty(df$y))) 

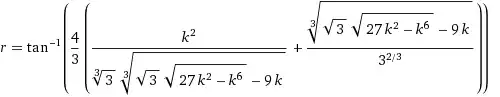
However, the model I have plotted is obviously not the same model as mod, there is no z and it is not quasiposson.

How can I plot something like the ggplot but using my actual model? I have looked at predict however, I am completely lost what to do when there is more than one explanatory, as in my case. I don't care about doing it in ggplot2

Answer 1

It would seems like you could trivially adapt your example to your new model by using stat_smooth(method='glm', family=quasipoisson, ...), but adding the z into the formula leads to errors. Looking from the ggplot2 docs, you can see that the predictdf is what is used to generate the limits for the intervals. Looking at the code for that function, it looks like it is only meant to work with predictions across the x dimension. But we can easily write our own version that works in multiple dimensions and then plot the limits as separate layers.

mypredictdf <- function (model, newdata, level=0.95){
  pred <- stats::predict(model, newdata = newdata, se =TRUE, type = "link")
  std <- qnorm(level/2 + 0.5)
  data.frame(newdata,
             y = model$family$linkinv(as.vector(pred$fit)),
             ymin = model$family$linkinv(as.vector(pred$fit - std * pred$se)),
             ymax = model$family$linkinv(as.vector(pred$fit + std * pred$se)), 
             se = as.vector(pred$se))
}
px <- with(df, seq(from=min(x), to=max(x), length=100))
pdf <- expand.grid(x=px, z=unique(df$z))
pdf <- mypredictdf(mod, newdata=pdf)
g <- ggplot(data=pdf, aes(group=z))
g <- g + geom_point(data=df, aes(x=x, y=y, color=z))
g <- g + geom_ribbon(aes(x=x, ymin=ymin, ymax=ymax),
                     alpha=0.2)
g <- g + geom_line(aes(x=x, y=y, color=z))

It seems like faceting would be a good idea:

g <- g + facet_wrap(~z)

Answer 2

Here is one approach that deals with multiple variables ( y = f(x,z) in your case).

mod <- glm(y ~ x + I(x^2) + z, family=quasipoisson, data = df)
pred <- predict(mod, type="response",se.fit=T)
df$pred <- pred$fit
df$se   <- pred$se.fit

ggplot(df, aes(x=y))+
  geom_point(aes(y=pred, color=z),size=3)+
  geom_errorbar(aes(ymin=pred-se, ymax=pred+se, color=z),width=1.5)+
  geom_abline(intercept=0, slope=1, color="blue", linetype=2)+
  labs(x="Actual", y="Predicted")

This plots predicted y vs. actual y, grouped by z, with error bars = ±1 × se. To get 95% CL on the predicted, you would need to use ±1.96 × se. The dotted line is a reference (actual = predicted) which would represent a perfect fit. You can see from this that z=b and z=c are problematic, but z in (a,d,e,f) all fit the data rather well.

If you have more than 2 variables, the grouping becomes problematic, but the asic approach of plotting predicted y vs. actual y still applies.