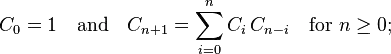Of course you can implement the catalan numbers in haskell (and I think as well the ml-family is powerful enough)!
But I guess this is not the answer you were looking for. So I hope you are familiar with the basic haskell syntax think of the catalan numbers as functions catalan :: Int -> Int any series of natural numbers is such a function (well for small indices). But as catalan numbers grow quite fast I will choose for the codomain of our function the type of Integers(= arbitrary big integral numbers).
catalan :: Int -> Integer
catalan 0 = 1
catalan n = sum [ ?catalan magic? | i <- [1..n]]
I know I almost solved the problem but there is still the catalan magic ;-) you have to do on your own.
But before I stop a few caveats
- this version of calculating the catalan numbers is far from optimal or efficient
- the case of negative input values is not taken care of.