looping through nodes and extract attributes in Networkx

Question

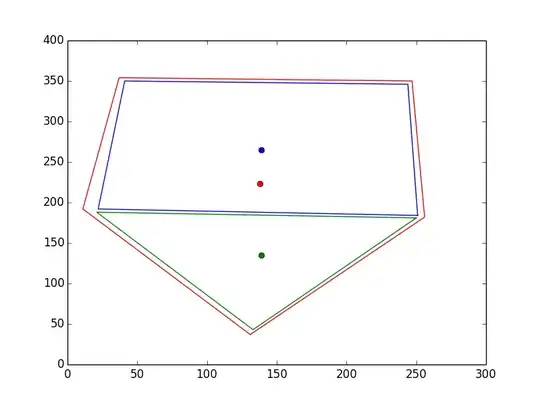
I defined in python some shapes with corresponding corner points, like this:

square = [[251, 184],
          [22, 192],
          [41, 350],
          [244, 346]]

triangle = [[250, 181],
            [133, 43],
            [21, 188]]

pentagon = [[131,  37],
            [11, 192],
            [37, 354],
            [247, 350],
            [256, 182]]

Then, I make use of NetworkX package to create a Graph:

G = nx.DiGraph()

Then, I create a node in the graph for each shape:

G.add_node('square', points = square, center = (139, 265))
G.add_node('triangle', points = triangle, center = (139, 135))
G.add_node('pentagon', points = pentagon, center = (138, 223))

Now is the problem, I have to create some edges connecting two nodes if a condition is satisfied. The condition to satisfy is if the center of a shape is inside or outside another shape, then create an edge like this:

G.add_edge('triangle', 'pentagon', relation = 'inside')
G.add_edge('triangle', 'square', relation = 'outside')

To do so, I have to loop through the nodes, extract the center of a shape, extract the points of the other shapes (NOT themselves, it's useless) and make the pointPolygonTest.

I've been trying quite much, but didn't came out with any solution. The closest (not really effective) solution I got is this:

nodes_p=dict([((u),d['points']) for u,d in G.nodes(data=True)])
nodes_c=dict([((u),d['center']) for u,d in G.nodes(data=True)])
for z,c in nodes_c.items():
    print z + ' with center', c
    for z,p in nodes_p.items():
        p_array = np.asarray(p)
        if cv2.pointPolygonTest(p_array,c,False)>=0:
            print 'inside ' + z
            #create edge
        else:
            print 'outside ' + z
            #create edge

This, gives me the following output, that is not optimal because there are some relation that should have been avoided (like triangle inside triangle) or some wrong relations (like pentagon inside square)

triangle with center (139, 135)
inside triangle
outside square
inside pentagon
square with center (139, 265)
outside triangle
inside square
inside pentagon
pentagon with center (138, 223)
outside triangle
inside square
inside pentagon

How can I solve this problem? Any suggestion is apreciated. Reminder: the main problem is how to loop through the nodes and extract the info. The packages I import for the whole script are:

import numpy as np
import networkx as nx
import cv2

Answer 1

Here is an image of your polygons

First, there is no need to cast the nodes as dictionaries, we can iterate on them directly. This code is based off of this example

for u,outer_d in G.nodes(data=True):
   center = outer_d['center']
   print u, "with center", center
   for v, inner_d in G.nodes(data=True):
        #Don't compare self to self
        if u != v:
            # Create a source image
            src = np.zeros((400,400),np.uint8)          
            # draw an polygon on image src
            points = np.array(inner_d['points'],np.int0)
            cv2.polylines(src,[points],True,255,3)
            contours,_ = cv2.findContours(src,cv2.RETR_TREE,cv2.CHAIN_APPROX_SIMPLE)
            if cv2.pointPolygonTest(contours[0],center,True) <= 0:
                print 'outside',v
            else:
                print 'inside',v

The output is

pentagon with center (138, 223)
inside square
outside triangle
square with center (139, 265)
inside pentagon
outside triangle
triangle with center (139, 135)
inside pentagon
outside square

Since the goal is to determine if one polygon is completely inside the other, we should check all of the vertices of one polygon are inside another. Here is a tentative (unfortunately untested) solution.

def checkPoint(point, poly,r=400):
    ''' determine if point is on the interior of poly'''
    # Create a source image
    src = np.zeros((r,r),np.uint8)       
    # draw an polygon on image src
    verts = np.array(poly,np.int0)
    cv2.polylines(src,[verts],True,255,3)
    contours,_ = cv2.findContours(src,cv2.RETR_TREE,cv2.CHAIN_APPROX_SIMPLE)
    return cv2.pointPolygonTest(contours[0],tuple(point),True) > 0:


for u,outer_d in G.nodes(data=True):
    points = outer_d['points']
    center = outer_d['center']
    print u, "with center", center
    for v, inner_d in G.nodes(data=True):
        poly = inner_d['points']
        if u != v:
            if all([checkPoint(point,poly) for point in points]):
                print 'inside',v
            else:
                print 'outside',v

The output for this example is as follows and now should be correct.

pentagon with center (138, 223)
outside square
outside triangle
square with center (139, 265)
inside pentagon
outside triangle
triangle with center (139, 135)
inside pentagon
outside square

Note that I have made the assumption that the polygons will be convex. If this is not true, then you could check all the points on the contour instead of just the corner points. You could also build in a convexity check using cv2, see this blog for details.